Elimination Method xy = 5 and 2x3y = 4LinkedIn Profilehttps//wwwlinkedincom/in/arunmamidi8ba/FaceBookhttps//wwwfacebookcom/arunkumarm1447Avail 25% off on study pack Avail Offer Solve by matrix inversion method 3x – y 2z = 13;

36 X Y 2 3x Y 35 X Y 5 2x Y 12 65 37 2x Chegg Com
X+y=5 2x-3y=5 by elimination method
X+y=5 2x-3y=5 by elimination method-Elimination Method xy = 5 and 2x3y = 4 Ch 3 Class 10 Maths xy=5 and 2x3y=4 solveQ Solve the following pair of linear equations by the Elimination meAdd the two equations together to eliminate x from the system 2x3y=5_2x5y=13_ 8y= 8 Divide each term in the equation by 8 y=1 Substitute the value found for y into the original equation to solve for x




Solve X Y 2 2x 3y 5 Brainly In
How do I solve these problems, I really need help Solve by substitution method 6x5y=17 x=538y Solve by elimination method 2x3y=5 4x6y=10 algebra Solve the following system using the substitution method 6x 2y = 4 y = 3x 2 algebra solve by substitution method 9x7y=4 x=234yDivide both sides by 2 Divide both sides by 2 \frac {2x} {2}=\frac {3y5} {2} 2 2 x = 2 3 y − 5 Dividing by 2 undoes the multiplication by 2 Dividing by 2 undoes the multiplication by 2 x=\frac {3y5} {2} x = 2 3 y − 5 x y = 5 ( equation 1 ) 2x 3y = 4 ( equation 2 ) Now, multiplying (eq1) by 2 and subtracting (eq2) from ( eq1 ) (2x 2y = 10) (2x 3y = 4 ) => 2x 2y 2x 3y = 6 => 5y = 6 => y = 6/5 Putting the value of y in ( eq1 )
2 algebraic methods (elimination and substitution) and graphical method Elimination 2x 3y = 5 So 6x 9y = 15 (equation 1) 3x y = 4 6x 2y = 8 (equation 2) (6x 9y) (6x 2y) = 15 8 7y = 7 y = 1 (equation 3) Substitute y = 1 into equation 2, 3x (1) = 4 x = 1 (x, y) = (1, 1) Substitution 2x 3y = 5 (equation 1) 3x y = 4, so y = 4 3x (equation 2)2x y – z = 3; Solve the following system of equations by elimination method x y = 5 2x – 3y = 4 pair of linear equations in two variables;
2 algebraic methods (elimination and substitution) and graphical method Elimination 2x 3y = 5 So 6x 9y = 15 (equation 1) 3x y = 4 6x 2y = 8 (equation 2) (6x 9y) (6x 2y) = 15 8 7y = 7 y = 1 (equation 3) Substitute y = 1 into equation 2, 3x (1) = 4 x = 1 (x, y) = (1, 1) Substitution 2x 3y = 5 (equation 1) 3x y = 4, so y = 4 3x (equation 2) Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving (3) and (2) by Elimination –5y = –6 5y = 6 y = 𝟔/𝟓 Putting y = 6/5 in (1) x y = 5 x 6/5 = 5 x = 5 – 6/5 x = (5 × 5 − 6)/5 x = (25 − 6)/5 x = 𝟏𝟗/𝟓 Hence, xSolve the following pair of linear equations by cross multiplying method 2x y = 5, 3x 2y = 8 > 10th > Maths > Pair of Linear Equations in Two Variables > Algebraic Methods of Solving a Pair of Linear Equations > Solve the following pair of
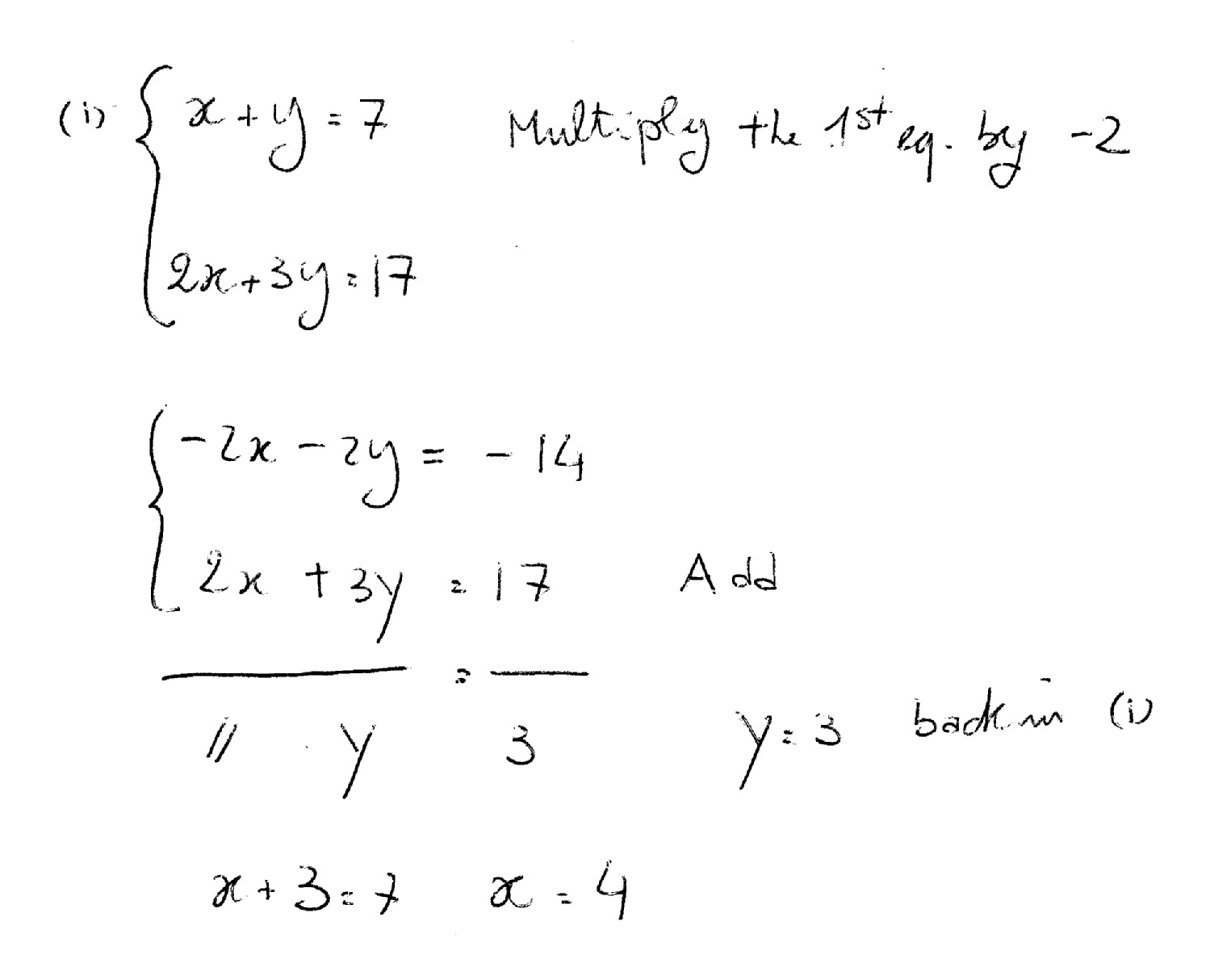



How Do You Solve The System Using The Elimination Method For X Y 7 And 2x 3y 17 Socratic




Solve 2x 3y 4 And 3x Y 5 By Elimination Method Brainly In
2x3Y13=0;3X5Y=16 stimulation method Xy=6 Xy=4 Find xy 1 8x5y=9 3x2y=4 linear equation 3x 4y =10 and 2x 2y = 2 When a two digit number is divided by the sum of its digits, the quotient is 7 If the ten's digit is diminished by twice the unit's digit, the remainder is zero What is the number? 2 x y = 5 1 2x 3y = 5 2 3x 3y = 15 multiply both sides to 2by 3 College Algebra Math Help Substitution Method Elimination Method Systems Of Equations By Elimination Algebra Word Problem Addition Method Systems Of Equations Finite Mathematics Word Problem Help RELATED QUESTIONSShare It On Facebook Twitter Email 1 Answer 1 vote answered by Chandan01 (511k points) selected Sep 30




Solving Systems Of Equations Algebraically Substitution Method The




Graph Graph Inequalities With Step By Step Math Problem Solver
Question 1262 Use elimination method in solving this;tnx x3y=5 2xy=5 Answer by jim_thompson5910 () ( Show Source ) You can put this solution on YOUR website! (x,y)=(4,1) x=2y6 in the second equation, define x in terms of y 2(2y6)3y=5 plug back into the first equation 4y123y=5 distribute 7y12=5 7y=7 y=1 solve for y Then, go back to the other equation and plug this value in for y x=2(1)6 x=26 x=4Solve by Addition/Elimination x4y6z=1 , 2xy2z=7 , x2y4z=5 x 4y 6z = 1 x 4 y − 6 z = − 1 , 2x y 2z = 7 2 x − y 2 z = − 7 , x 2y 4z = 5 − x 2 y − 4 z = 5 Choose two equations and eliminate one variable In this case, eliminate x




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




1 Using The Elimination Method Solve Each Of T Gauthmath
Solve the following pair of linear equations by the elimination method and the substitution method x y = 5 and 2x – 3y = 4 0 CBSE CBSE (English Medium) Class 10 Solve by substitution and equating method xy=5 2x3y=4 Share with your friends Share 0 The give equation is ,Solution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0




Solved By Elimination Method 2x Y 5 And 3x 2y 8 Brainly In




Systems Of Equations Substitution Method Ppt Video Online Download
Question 1 Solve the following systems of linear equations by Gaussian elimination method 2x − 2y 3z = 2, x 2y − z = 3, 3x − y 2z = 1Systemofequationscalculator elimination method x2y=2x5, xy=3 en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set ofThe elimination method of solving systems of equations is also called the addition method To solve a system of equations by elimination we transform the system such that one variable "cancels out" Example 1 Solve the system of equations by elimination $$ \begin{aligned} 3x y &= 5 \\ x y &= 3 \end{aligned} $$



The Elimination Method




Solve X Y 5 And 2x 2y 10 By Elimination Method Brainly In
Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystepIn detail steps i will show you how to solve the equation in elimination method! Hi, here are the answers 1)Solve by the elimination method 2x3y=5 and 4x6y=10 Answer infinitely many solutions 2)Solve using the multiplication principle 2x>1/9 The solution set is {xx < or >?




Solve The Following System Using Gauss Elimination Method X 8y Z




Chapter 9 Systems Of Linear Equations Pdf Free Download
X 3y – 5z = 8 asked in Matrices and Determinants by nchi ( 4k points) matricesClick here👆to get an answer to your question ️ Solve by elimination method x y = 5 2x 3y = 4 Join / Login > 10th > Maths > Pair of Linear Equations in Two Variables Solve by elimination method x y = 5 2 x − 3 y = 4 Easy Answer x y = 5 Free PDF Download of CBSE Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Multiple Choice Questions with Answers MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern Students can solve NCERT Class 10 Maths Pair of Linear Equations in Two Variables MCQs with Answers to know their preparation level




Show Graphically That The System Of Linear Equations 2x 3y 5 6y 4x 3 Youtube




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y
Solve by using Elimination method xy=5, 2x3y = 5 1 See answer kcanupa2 is waiting for your help Add your answer and earn points mohit mohit Answer New questions in Math Example 12 Use elimination method to find all possible solutions of the following pair of linear equations 2x 3y = 8 4x 6y = 7 2x 3y = 8 4x 6y = 7 We multiply (1) by 2 2 (2x 3y) = 2 × 8 4x 6y = 16 We use elimination method with equation (3) & (2) 0 = 9 Since this is not true Hence, the equation has no solution Solve by the elimination method 2x 3y = 5 4x 6y = 10 Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our website By continuing to use this site you consent to the use of cookies on your device as described in our cookie policy unless you have disabled them




3 X 4y 4 X Y 5 5 4x 3y 4 2x Y 10 4 10 2x Chegg Com




X Y 5 2x 2y 10 Elimination Method Novocom Top
Solve the system of equations 2x3y=5 and 4xy= 3 solve this system of equations by using the substitution method 5x3y=11 (1) and 3x22y=1 (2)1 Solve the system using substitution method 2x 3y = 5 x y = 5 2 Solve using elimination my addition method 4x 3y = 8 5x 6y = 1 3 Solve for (x,y,z) 3x 2yz = 2 4x y 2z = 11 3x 2y z = 6 4 Solve, list all ordered pairs separately 3x2 y2 = 18 2x2 3y2 = 10 5 Graph the ellispe by showing all 4 vertices and the 2 foci points\\begin{aligned}&x2y=10\\&2xy=5\end{aligned}\ > <




X Y 5 2x 2y 10 Elimination Method Novocom Top




Elimination Method Day 1 Ppt Download
Gauss Elimination Method with Example Let's have a look at the gauss elimination method example with a solution Question Solve the following system of equations x y z = 2 x 2y 3z = 5 2x 3y 4z = 11 Solution Given system of equations are x y z = 2 x 2y 3z = 5 2x 3y 4z = 11 Let us write these equations in1 Solve the system of linear equations using the GaussJordan elimination method x 2y = 17 2x 3y = 29 2 Solve the system of linear equations using the GaussJordan elimination method 3x 2y = 0 2x y = 5 x 2y = 4Subtract 3y from both sides Subtract 3 y from both sides 2x=53y 2 x = 5 − 3 y Divide both sides by 2 Divide both sides by 2 \frac {2x} {2}=\frac {53y} {2} 2 2 x = 2 5 − 3 y Dividing by 2 undoes the multiplication by 2




Introductory Algebra Chapter 4 95 F Equations And Chegg Com
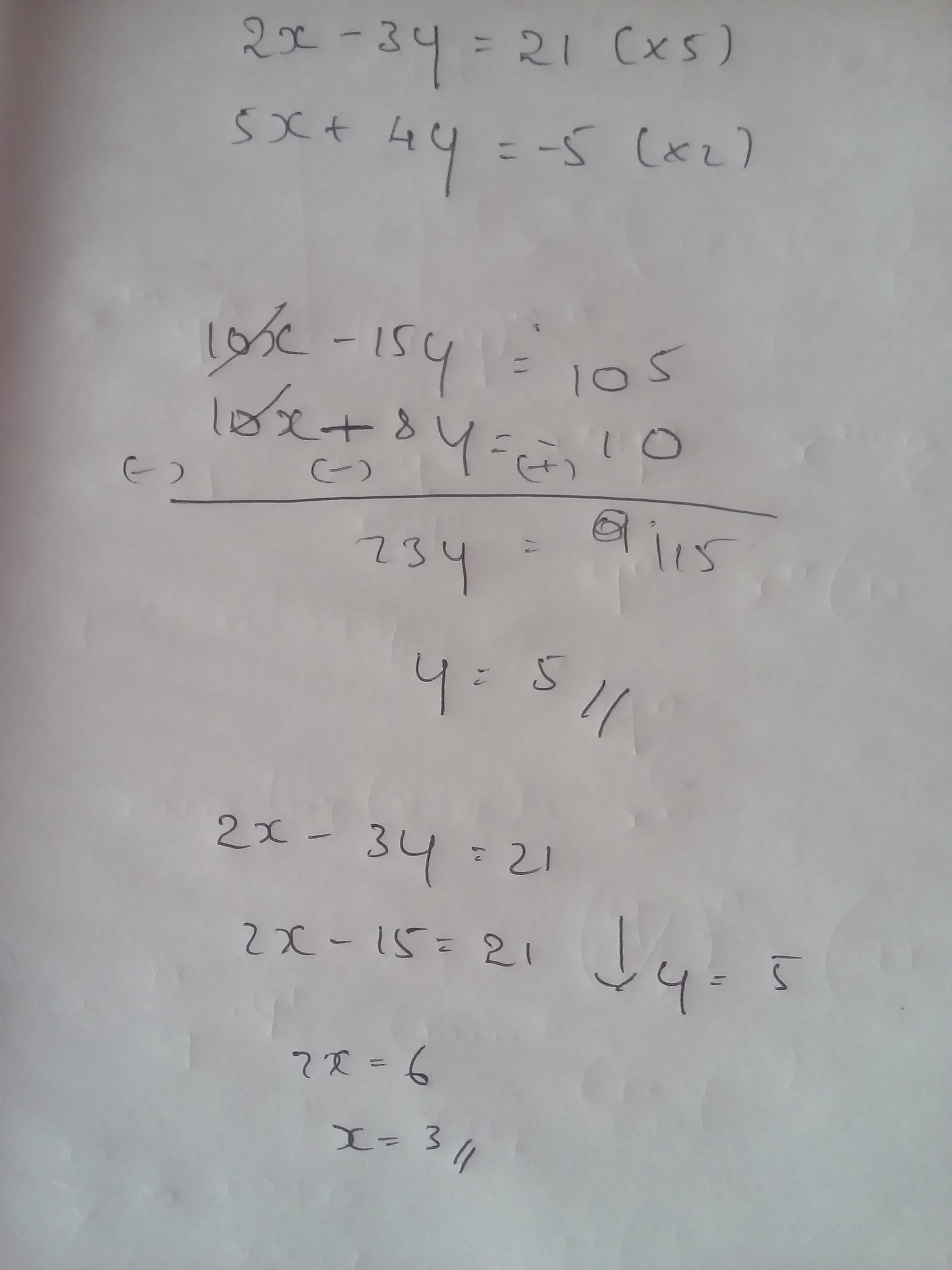



How Do You Solve 2x 3y 21 And 5x 4y 5 Socratic
Get an answer for 'If 2x3y= 5 and x3y= 4 find the values of x and y' and find homework help for other Math questions at eNotesSolve the following equations by substitution method 5 x 3 y 8 = 0 and 2x 3 y 5 = 0 Solution Question 2 Solve the following equations using substitution method 5x 3y 8 = 0 and 2x 3y 5 = 0 Solution Question 3 Solve the following equations by substitution method y = 6x 11 and 2x 3y = 7 SolutionStart with the given system of equations Multiply the both sides of the first equation by



Using Gaussian Or Gauss Jordan Elimination X Y Z 5 2x 3y 6z 32 4x 5y 10z 8 Mathskey Com




G 1 Coaching Class 3rd Chapter Pair Of Linear Equation In Two Variable
Solution Step 1 Select a variable which you want to eliminate from the equations Let us select y y 4x−3y = 32 xy = 1 4 x − 3 y = 32 x y = 1 Step 2 Take suitable constants and multiply them with the given equations so as to make the coefficients ofSolve the following pair of linear equations by elimination method xy=5 and 2x3y=4 Solve for x and y, using substitution method 2x y = 7, 4x 3y 1 =0 Solve the silultaneous equations by using Graphical method xy =7 , 2x 3y = 9Find the value of x given the system of equations below 2x3y = 5 5x−2y = −16 2 x 3 y = 5 5 x − 2 y = − 16 Elimination Method for a System of Two Equations The elimination method works by



Systems Of Linear Equations




X Y 5 And 2x 3y 4 Solve By Elimination Method Brainly In
Answer to Solve the following pair of linear equations by the elimination method and the substitution method x y = 5, \\2x 3y = 4 By signingSolve for x and y, using substitution method 2x y = 7, 4x 3y 1 =0 Solve the following pairs of equation by elimination method x y = 6 2x 3y = 4 Solve the following pair of linear equations by elimination method xy=5 and 2x3y=4 x 2y 5 3x 2 3y 10 solve by elimination method Mathematics TopperLearningcom dzs9yv22 Starting early can help you score better!




X Y 5 2x 2y 10 Elimination Method Novocom Top




Use Gaussian Elimination Method To Solve The Chegg Com
2y x = 3 3y 2x = 5 Solve by Substitution // Solve equation 1 for the variable x 1 x = 2y 3 // Plug this in for variable x in equation 2 2 2• (2y3) 3y = 5 2 y = 1 // Solve equation 2 for the variable y 2 y = 1 // By now we know this much x = 2y3 y = 1 // Use the y value to solve for xAll x in I, then the sequence of approximations x1,x2, xn will converge to α, if the initial starting value x0 is chosen in I 6 What is the order of convergence for fixed point iteration?Solve by Addition/Elimination 2x3y=6 , 2x3y=6 2x 3y = 6 2 x 3 y = 6 , 2x − 3y = 6 2 x 3 y = 6 Add the two equations together to eliminate y y from the system 2 2 x x 3 3 y y




Solve X Y 5 And 2x 3y 4 Novocom Top




X Y 5 2x 3y 4 Solve By Elimination Method
Solve the following simultaneous equations2xy=5;The convergence is linear and the convergence is of order 1 7 Solve xy = 2, 2x3y = 5 by Gauss Elimination method Given xy = 2, 2x3y = 5 When using Gaussian elimination to solve a system of linear equations, explain how you can recognize that the system has no solution math help please solve the system by the elimination method 5x3y=13 & 7x2y=11 math Solve the system of equations by elimination (2 marks) y=2x^22x3 y=x^22x3



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




Solving Systems Of Equations Using Linear Combinations
By solving this equation by eliminating method y and y would get canceled, leaving 2x 3x = 5 10 5x = 15 x = 3 By putting value of x in equation 1, 2x y = 5 2 × 5 y =




I 2xy5 3x Y5 See How To Solve It At Qanda




Ex 3 4qno1 1 Solve X Y 5 2x 3y 4 By The Elimination Method Youtube




X Y 5 And 2x 3y 4 Using Elimination And Substitution Method Brainly In




Urgent 10 X Y 2 X Y 4 15 X Y 5 X Y 2 Solve By Elimination Method Maths Pair Of Linear Equations In Two Variables Meritnation Com
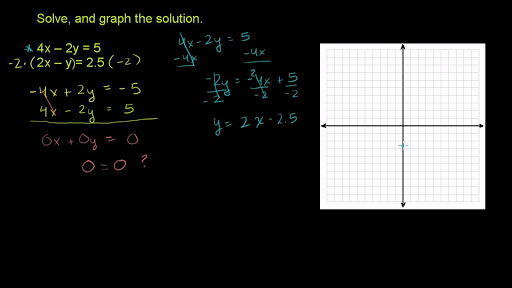



Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Solve X Y 2 2x 3y 5 Brainly In




Math 163 Online Problems Supplemental Lessons On Gaussian




X Y 5 2x 2y 10 Elimination Method Novocom Top




Use Gauss Jordan Elimination To Solve For All Chegg Com



Q Tbn And9gcqxnk Lpfjle Erogd0wsraw D67yjyrnkghuofquiwt4u Rzfp Usqp Cau



2



X Y 5 And 2x 3y 4 व ल पन व ध Elimination Method व ल पन व ध स हल क स कर 10th क ल स Youtube




4x 3y 5 5 2x Y 4 By Elimination Method Brainly In




Bsolve The System Oflinear Eq See How To Solve It At Qanda




Practice Problems Mat110 Chapter 9




Solve By Elimination Method X Y 5 2x 3y 5 Brainly In




2x 3y 4 0 3x Y 5 0 Youtube
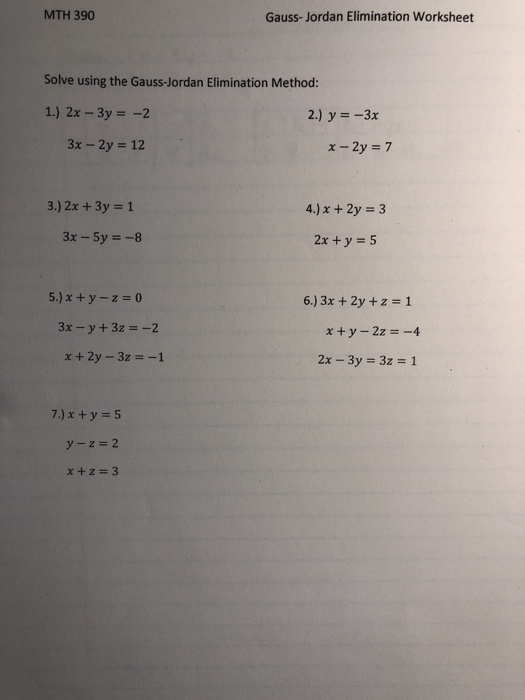



Mth 390 Gauss Jordan Elimination Worksheet Solve Chegg Com




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




Problem Set 6b Mathchamber




How To Solve Pair Of Linear Equations By Any Suitable Method X Y 5 2x 3y 5 Brainly In




ロイヤリティフリーxy5 2x 3y5 最高のぬりえ




36 X Y 2 3x Y 35 X Y 5 2x Y 12 65 37 2x Chegg Com




Solve For Lines Of Equation X Y 5 0 And 2x 2y 10 0 Youtube
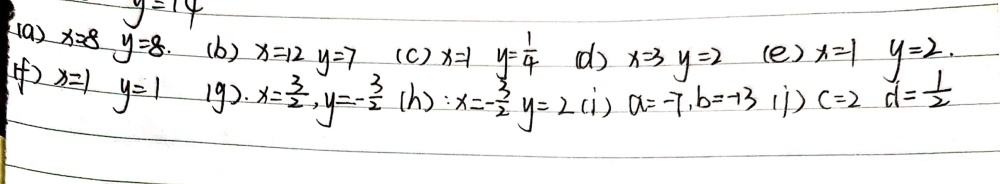



2 Using The Elimination Method Solve Each Of Li Gauthmath




Solve 2x Y 5 And 3x 2y 8




Algebraic Elimination Method Class 10 Ncert Solutions Suresolv




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




Homework Lesson 4 Solve Each System Using The Chegg Com




1 Solve The Following Systems Of Linear Equations Chegg Com




Solve X Y 5 And 2x 2y 10 By Elimination Method Brainly In




1 Solve The Following Pair Of Linear Equations By Method X Y 5 And 2x




X Y 5 2x 3y 4 Solve Using Elimination And Cross Multiplication Method Maths Pair Of Linear Equations In Two Variables Meritnation Com



Q Tbn And9gcsiqepudqftkrf4g Cwpyf2oujyvsrwjuvibffqjqm02x0mpmvd Usqp Cau
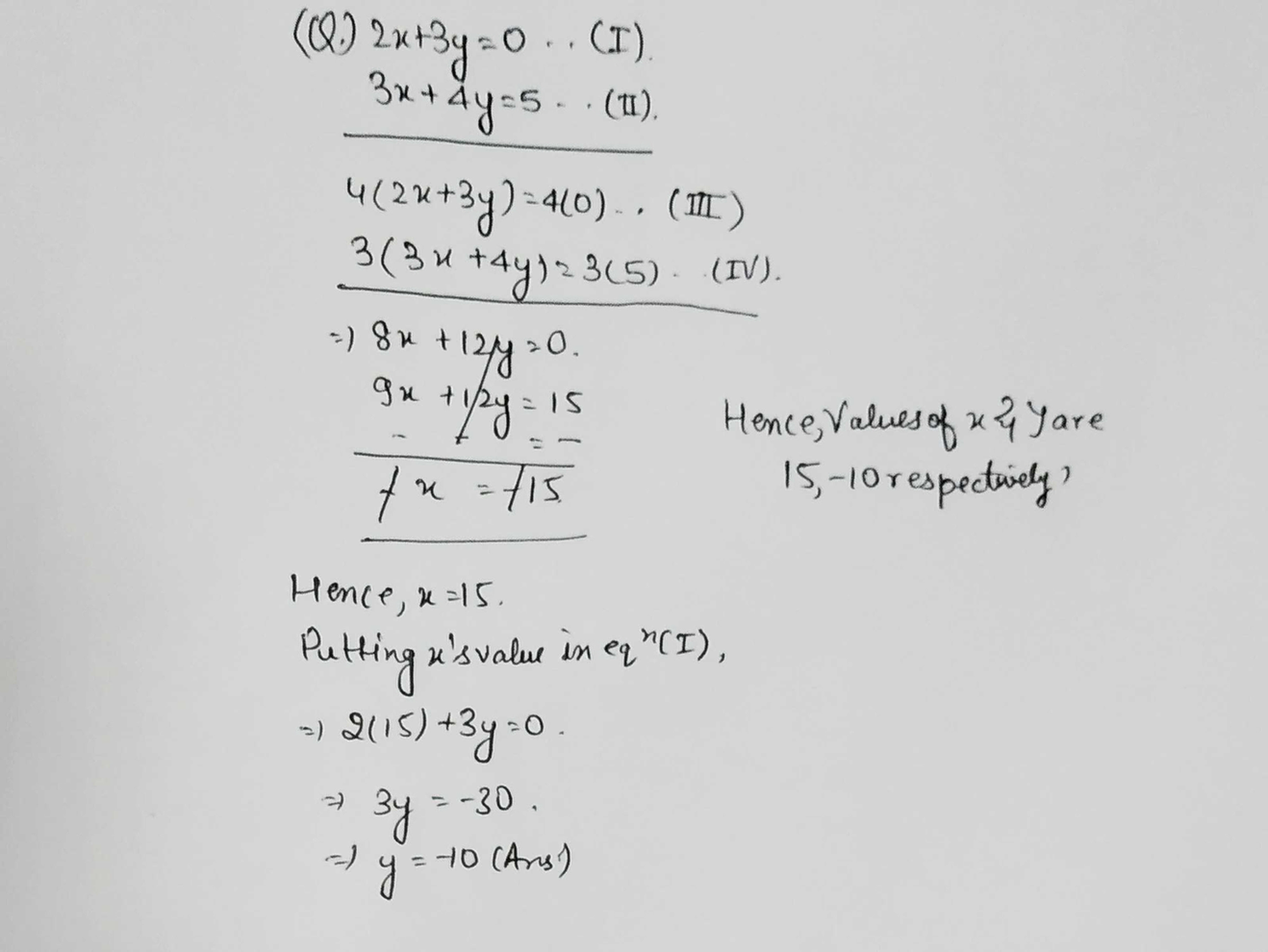



2x 3y 0 And 3x 4y 5 By Elimination Method Scholr




Solve For X And Y 15 X Y 22 X Y 5 40 X Y 55 X Y 13 X Y And X Y
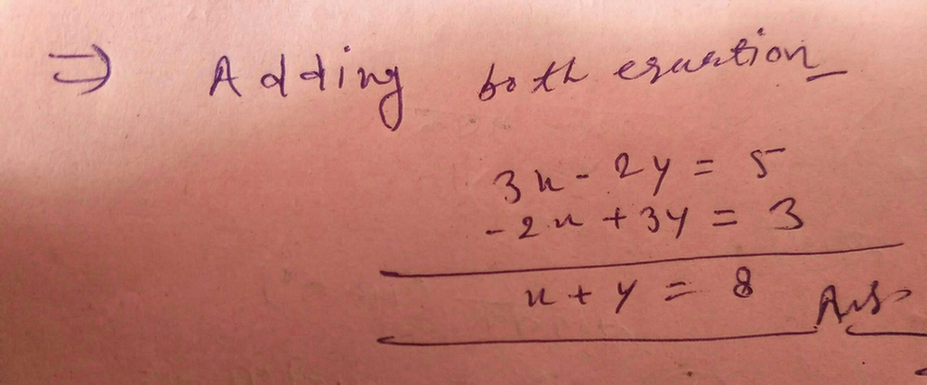



If 3x 2y 5 And 3y 2x 3 Then Find The Value Of X Y Scholr




Use The Elimination Method A 2x 3y 5 3 2y 14 B 2x



2




Ncert Solutions For Class 10 Maths Pair Of Linear Equation Flickr




X Y 5 2x 3y 4 व ल पन व ध Elimination Method Malhargarh Education Center Youtube



2




Solve By Elimination Method 1 X 3y 7 And X Y 5 2 8x 5y 9 And 3x 2y 4 3 3x Y 3 And 4x Y 8 Brainly In



How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora




Ppt System Of Equations And Elimination Powerpoint Presentation Free Download Id
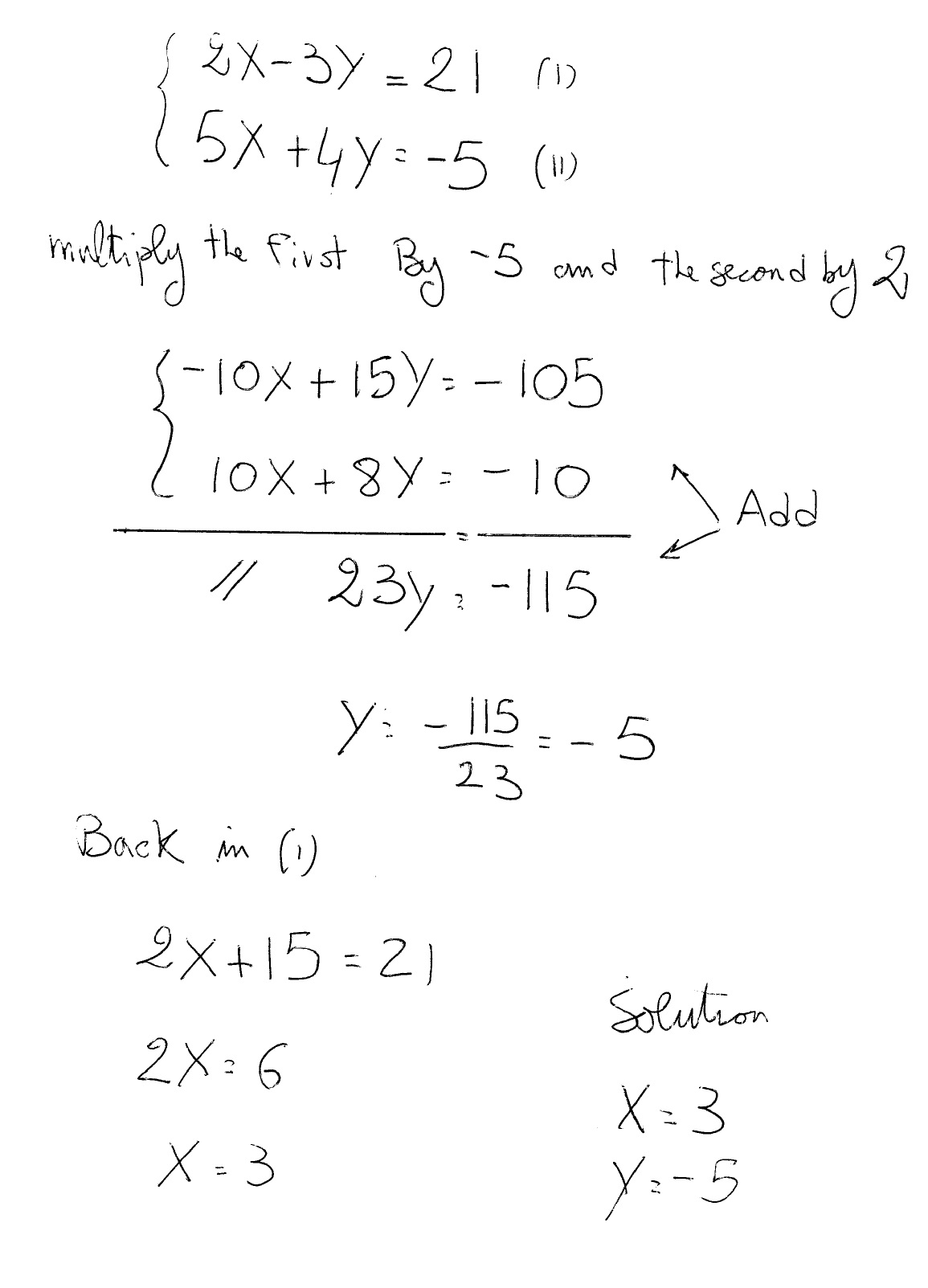



How Do You Find The Solution Of The System Of Equations 2x 3y 21 And 5x 4y 5 Socratic




Elimination Method X Y 5 And 2x 3y 4 Youtube




Ex 4 6 3 Examine Consistency X 3y 5 2x 6y 8 Ex 4 6
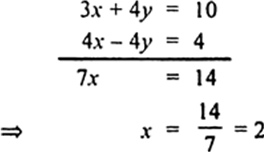



Solve The Following Pair Of Linear Equations By The Elimination Method And The Substitution Methodx Y 5 And 2x 3y 4



X Y 25 And X Y 5 What Is The Value Of X And Y Quora



Q Tbn And9gcsbc66bzmn2moq Jih Rhlwfi6kbfjoqcq Pqgcwyd5b6pu3z12 Usqp Cau




Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations



What Is The Answer To Find The Equation Of A Straight Line Through The Point Of Intersection Of Lines 2x 3y 5 0 And 3x 4y 7 0 Which Is Parallel To The Line 2x Y 2 0 Quora




X Y 5 2x 2y 10 Elimination Method Novocom Top



Solve For X And Y 5 X 3 Y 1 3 2x 2 3y 5 Sarthaks Econnect Largest Online Education Community




Simultaneous Equations 1 Ppt Download




Solve Graphically X Y 5 And 2x 3y 4 Novocom Top



Q Tbn And9gcsiqepudqftkrf4g Cwpyf2oujyvsrwjuvibffqjqm02x0mpmvd Usqp Cau




Systems Of Equations With Elimination 3y 4x 11 Y 2x 13 Video Khan Academy




Elimination Method Day 1 Ppt Download




Substitution Method X Y 5 And 2x 3y 4 Youtube




In Problems 7 10 Solve The Systems Of Equations By Chegg Com




Two Linear Equations In The Same Two Variables Are Called Linear Equation In Two Variables The Most General Form Of A Pair Of Linear Equations Is A Ppt Download




ロイヤリティフリーxy5 2x 3y5 最高のぬりえ



Solve The Following System Of Equations By Elimination Method X Y 5 2x 3y 4 Sarthaks Econnect Largest Online Education Community




Solve X 2y 1 2x Y 7 Maths Questions
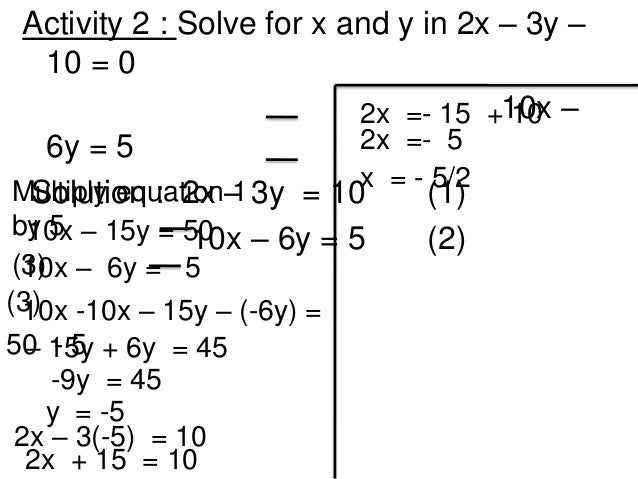



Simultaneous Equations




2x Y 5 X Y 1 Solve By Matrix Est So28 Ty 5 Nat 1vloot Jon Wove



2
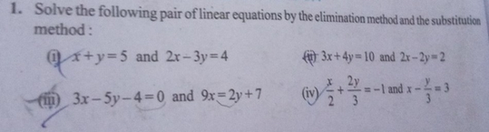



1 Solve The Following Pair Of Linear Equations By The Elimi Scholr



0 件のコメント:
コメントを投稿