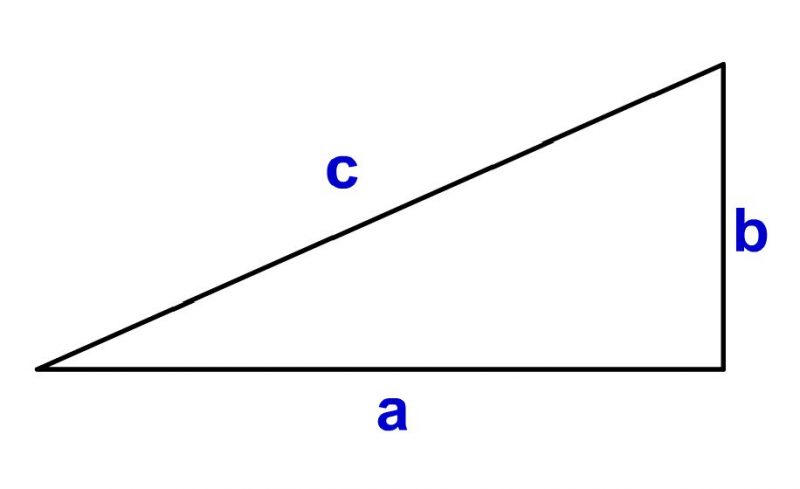
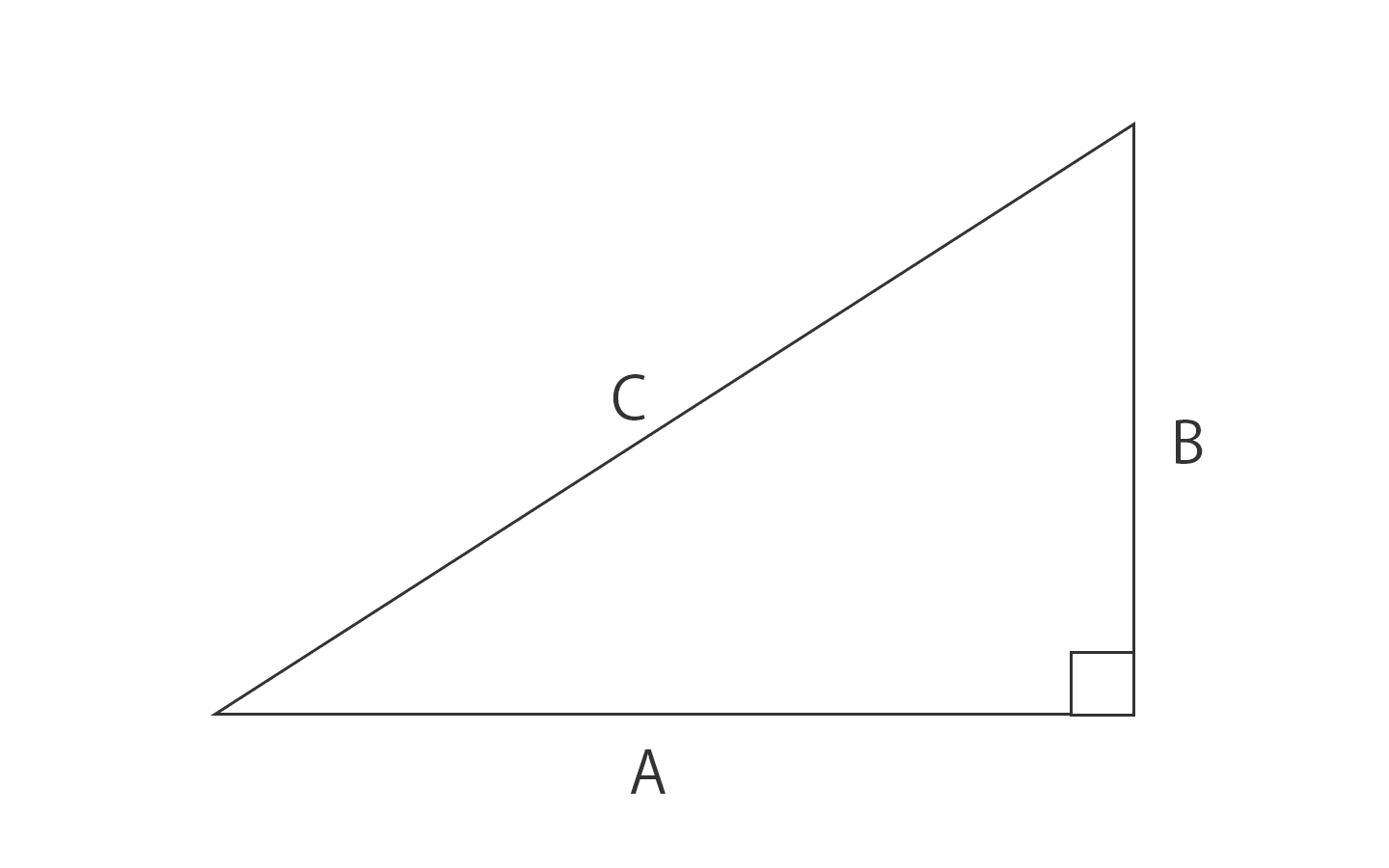
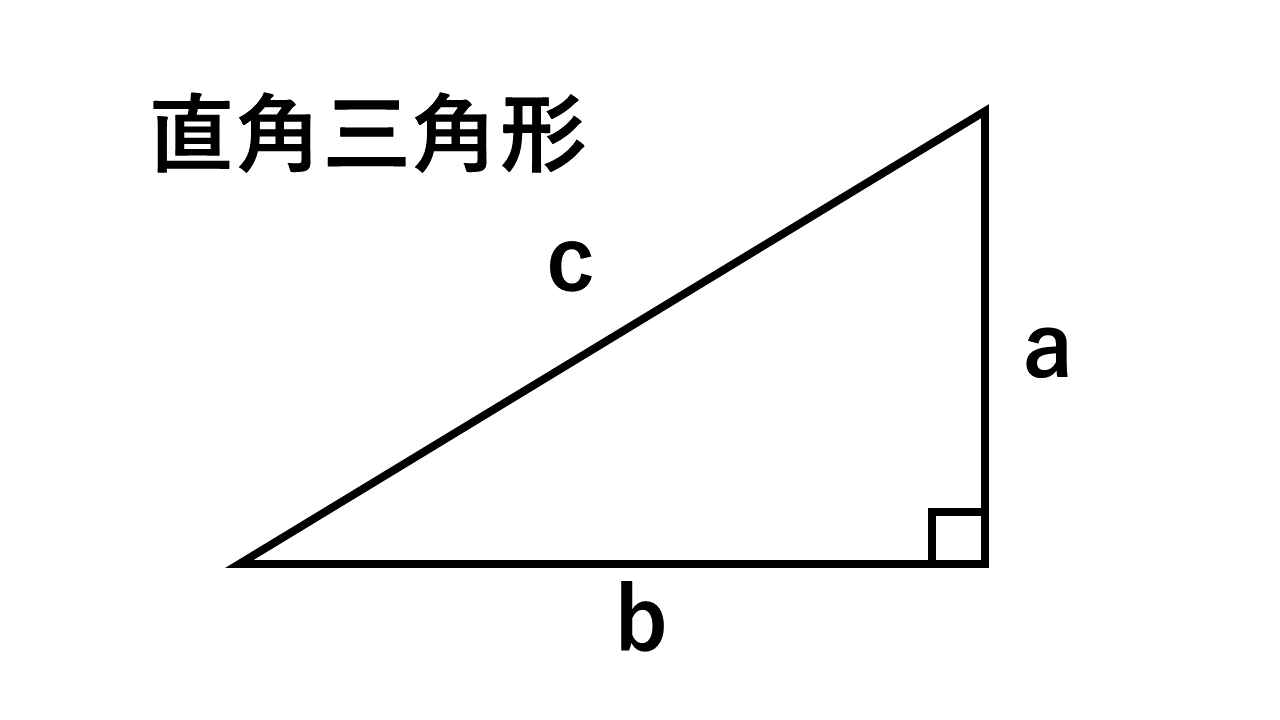
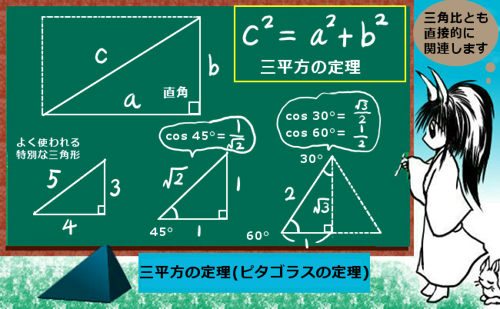
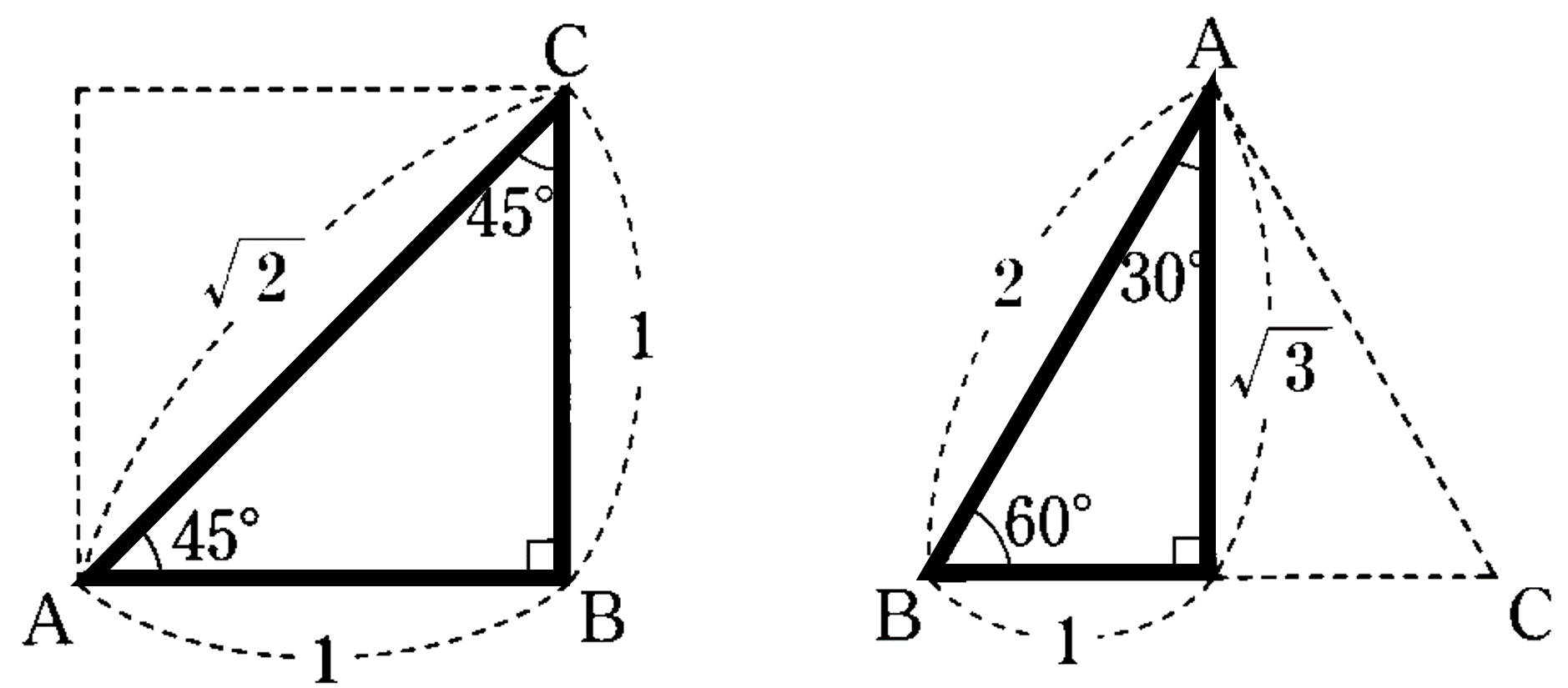
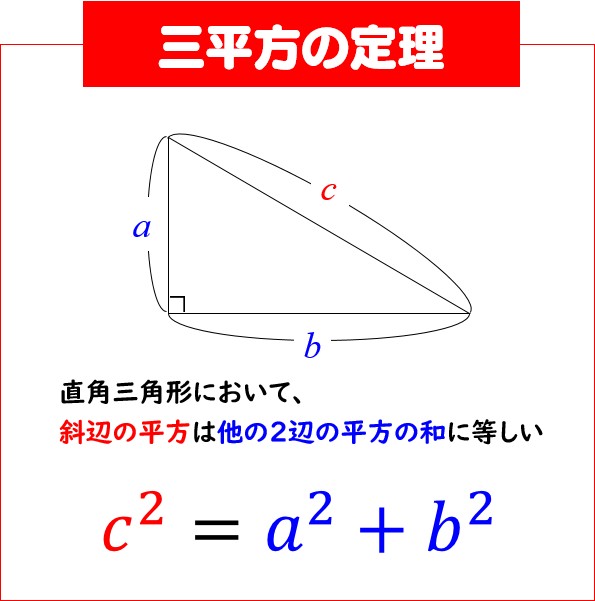
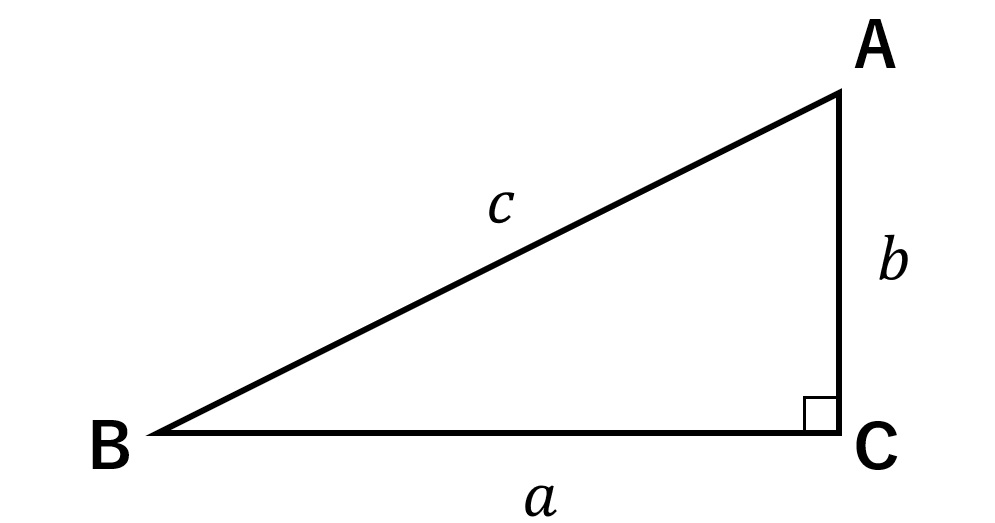
三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。Nov 29, 16 · 中3数学では、 三平方の定理(ピタゴラスの定理) を勉強してきたよな? 簡単に復習すると、 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、 a²+ b² = c² が成り立つ ってやつだったな。 さあ、この定理を使いこなせるようになるんだぞ。 今回はそのための基礎トレーニングだ。三 平方 の 定理 直角 三角形45°:45°:90°の直角三角形 こちらは直角以外の2角が2つとも45°になっている三角形、すなわち直角二等辺三角形です。これは辺の比が1:1:√2になります。 この三角形の角度と辺の比も必ず覚えておくようにしましょう。
三平方の定理の導入 Geogebra
直角三角形 三平方の定理
直角三角形 三平方の定理-ケプラー三角形は三辺の比が等比数列となっている直角三角形で、その公比は黄金比 の平方根 であるような三角形のことである。 つまりケプラー三角形の辺の比は 、おおよそ1 :1272 :1618 である。 したがって三角形の一辺を辺とした正方形も黄金比を公比とした等比数列になる。直角三角形的一个锐角的邻边和斜边的比值叫这个锐角的余弦值 编辑本段 余弦定理性质 对于任意三角形,任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的两倍积,若三边为a,b,c 三角为A,B,C ,则满足性质




数学 中3 61 三平方の定理 基本編 Youtube
Dec 07, · 今回は「直角三角形TOP7」と題して、三平方の定理にまつわるお話をしていきます。 三平方の定理は、直角三角形の斜辺の2乗が他の辺の2乗の和に等しい、という公式です。頂点Aから垂線をおろして直角三角形をつくる。 三平方の定理に当てはめる。 x 2 1 2 =3 2 x 2 =91 x 2 =8 x=±2 2 x>0よりx=2 2 答 2 2 cm 確認次のそれぞれの三角形で、頂点Aから辺BCにおろした垂線の長さを求めよ。 答表示 1辺8cmの正三角形 A B C 4 3 cm AB=AC=29cm, BC=40cmSep 11, · 一、直角三角形 勾股定理及其逆定理 (1)勾股定理:直角三角形两条直角边的平方和等于斜边的平方。 (2)勾股定理的应用:①已知直角三角形的两边求第三边; ②已知直角三角形的一边,求另两边的关系;③用于证明有关线段平方关系的问题。 (3
直角三角形の直角をはさむ2辺の長さを a,b とし、斜辺の長さを c とすると、次の関係が成り立つ。 c 2 = a 2 b 2 {\displaystyle c^{2}=a^{2}b^{2}} この定理を証明したのは古代ギリシアの数学者ピタゴラスであるとも言われているので、この定理は「ピタゴラスの定理Fcst 1年前 已收到1个回答 我来回答 举报 赞 恋曲18 花朵 共回答了15个问题 采纳率:100% 向TA提问 举报 (用解析几何的方法证) 设三角形三个顶点为 (x1,y1), (x2,y2), (x3,y3) 平面上任意一点为(x,yDec 23, · Pythagorean theorem は直角三角形の3辺の長さの関係を表す 斜辺の長さを c 他の2辺の長さを a b とすると定理は が成り立つという等式の形で述べられる 三平方の定理さんへいほうのていり勾股弦の定理こう
Jul 01, 21 · 例2:(1)解:上述解法是不对的.因为a=10 ,b=8 ,c=6 ,b2+c2=64+36=100=102=a2 ,即b2+c2=a2.所以由a ,b ,c组成的三角形两边的平方和等于第三边的平方 ,利用勾股定理的逆定理可知a ,b ,c可构成直角三角形 ,其中a是斜边 ,b ,c是两直角Sep 29, 19 · 直角三角形边长公式:c²=a²b² ,已知三角形两条直角边的长度 ,可按公式c²=a²b²计算斜边。 直角三角形边长关系 1、两边之和大于第三边 2、直角三角形中两直角边的平方和等于斜边的平方(c²=a²b²) 30度直角三角形边长,30度角所对的直角边是斜边的一半Dec 15, 16 · 46勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2b^2=c^2 47勾股定理的逆定理 如果三角形的三边长a、b、c有关系a^2b^2=c^2 ,那么这个三角形是直角三角形 48定理 四边形的内角和等于360° 49四边形的外角和等于360°
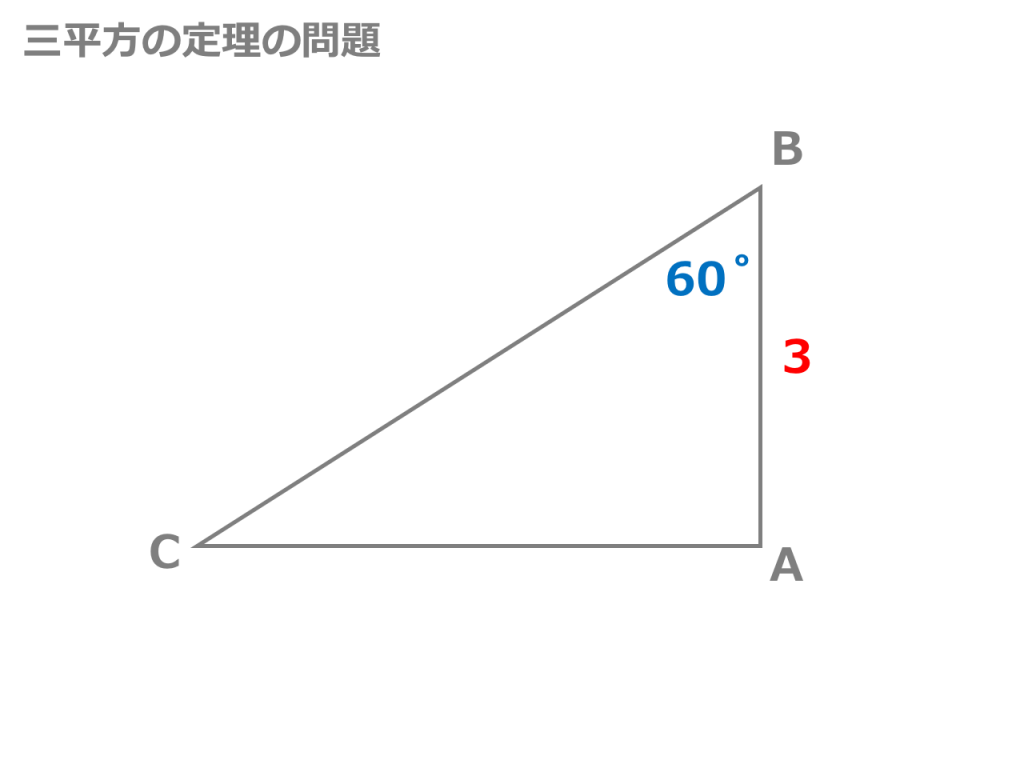



3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理 おやじさん ネット
Mar 17, · 1 直角三角形的性质 1、直角三角形两直角边的平方和等于斜边的平方。 ∠BAC=90°,则AB²AC²=BC²(勾股定理) 2、在直角三角形中,两个锐角互余。 如图,若∠BAC=90°,则∠B∠C=90° 3、直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位直角三角形特殊性质 编辑 语音 它除了具有一般三角形的性质外,具有一些特殊的性质 : 1、 直角三角形两直角边的平方和等于斜边的平方。 如图2,∠BAC=90°,则AB²AC²=BC²( 勾股定理) 2、在直角三角形中,两个锐角互余。 如图2,若∠BAC=90°,则∠B∠C=90° 3、直角三角形中, 斜边 上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点, 外接圆 半径R=C/2与三角形有关的定理: 15 定理 三角形两边的和大于第三边 16 推论 三角形两边的差小于第三边 17 三角形内角和定理 三角形三个内角的和等于 180° 18 推论 1 直角三角形的两个锐角互余 19 推论 2 三角形的一个外角等于和它不相邻的两个内角的和 推论 3 三角形的一个外角大于任何一个和它不相邻的




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




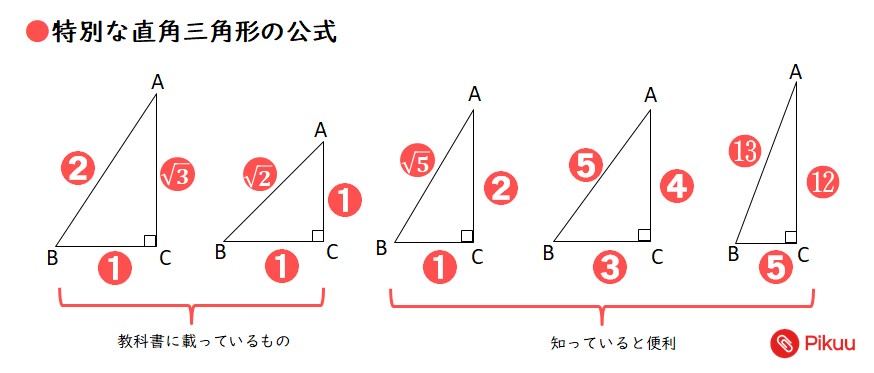
中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
次のような直角三角形の3辺の長さについては, a 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.)直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 となります。 となります。 が成り立ちます。 これを「三平方の定理」 といいます。Aug 16, · 直角三角形じゃないのに三平方の定理が使えるのは何故ですか?それは3平方の定理ではなく余弦定理といいます abcに対してbc^2=ab^2ac^22abaccos∠bacが成り立つ∠bac=90°の時 abcは直角三角形となりcos∠bac=0となり3平方の定理




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
直角三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と角度 斜辺と高さ 斜辺と角度 高さと角度 面積と底辺 面積と高さ 面積と斜辺 面積と角度三角形五心定律内心定理 编辑 三角形内切圆的圆心,叫做三角形的内心。 内心的性质: 1、三角形的三条内 角平分线 交于一点。 该点即为三角形的内心。 2、 直角三角形 的内心到边的距离等于两直角边的和与斜边的差的二分之一。 3、P为ΔABC所在空间中任意一点,点0是ΔABC内心的充要条件是: 向量 P0= (a×向量PAb×向量P×向量PC)/ (abc) 4、O为三角形的内心,A、BMay 15, · 1、勾股定理,直角三角形两直角边的平方和等于斜边的平方。 2、在直角三角形中,两个锐角互余。 3、直角三角形中,斜边上的中线等于斜边的一半,即为直角三角形斜边中线定理。 4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
有一个角是45度直角三角形三条边比例是多少 假设等于单位1,则根据勾股定理有一个角是45°的直角三角形,也就是根号2那么两直角边相等比例为11,是等腰直角三角形,则斜边=1的平方1的平方的和的平方勾股弦为什么中国古代叫直角三角形的边"勾股弦"? 急 勾股定理又称毕达哥拉斯定理,其内容是:一个直角三角形斜边的平方,等于其两个直角边的平方和 其实汉漠拉比时代的巴比伦人早就发现了这一定理,而毕达哥拉斯只不过是第一个对这一定理作了证明的Nov 15, 19 · 直角三角形 性质1:直角三角形两直角边的平方和等于斜边的平方。 性质2:在直角三角形中,两个锐角互余。 性质3:在直角三角形中,斜边上的中线等于斜边的一半。 性质4:直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。 等腰直角三角形




A1 Abc 3 P Q R Lihat Cara Penyelesaian Di Qanda



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方
座標上での2点間の 三平方の定理とは、直角三角形の三辺の長さに関する定理である。 斜辺の2乗は他の2辺の2乗の和に等しくなる。 三角形の三辺をa,b,cとし、斜辺がcとするとc^2=a^2b^2となる。Jan 01, 21 · 若两条直角边不一样长,短的那条边叫作"勾",长的那条边叫作"股" 。 直角三角形满足 毕氏定理 (勾股定理),即两直角边边长的 平方 和等于斜边长的平方。Jul 01, 21 · 三角形三边关系是三角形三条边关系的定则,具体内容是在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。 设三角形三边为a,b,c则ab>c,a>cb,bc>a,b>ac,ac>b,c>ba 直角三角形 性质1直角三角形两直角边的平方和等于斜边的平方。 性质2在




直角三角形の辺の長さ 合同条件 面積について アタリマエ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
May 10, 21 · 三 平方 の 定理 応用 三 平方 の 定理 応用 解き方 三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 数学史から入る46勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2b^2=c^2 47勾股定理的逆定理 如果三角形的三边长a、b、c有关系a^2b^2=c^2 ,那么这个三角形是直角三角形 86 平行线分线段成比例定理 三条平行线截两条直线,所得的对应 线段成比例May 28, 21 · 《直角三角形》教案教学目标:1、了解勾股定理及其逆定理的证明方法2、结合具体例子了解逆命题的概念,会识别两个互逆命题、知道原命题成立其逆命题不一定成立。教学重点、难点:进一步掌握演绎推理的方法。教学过程:一、温故知新1、你记得勾股定理的内容吗?




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ
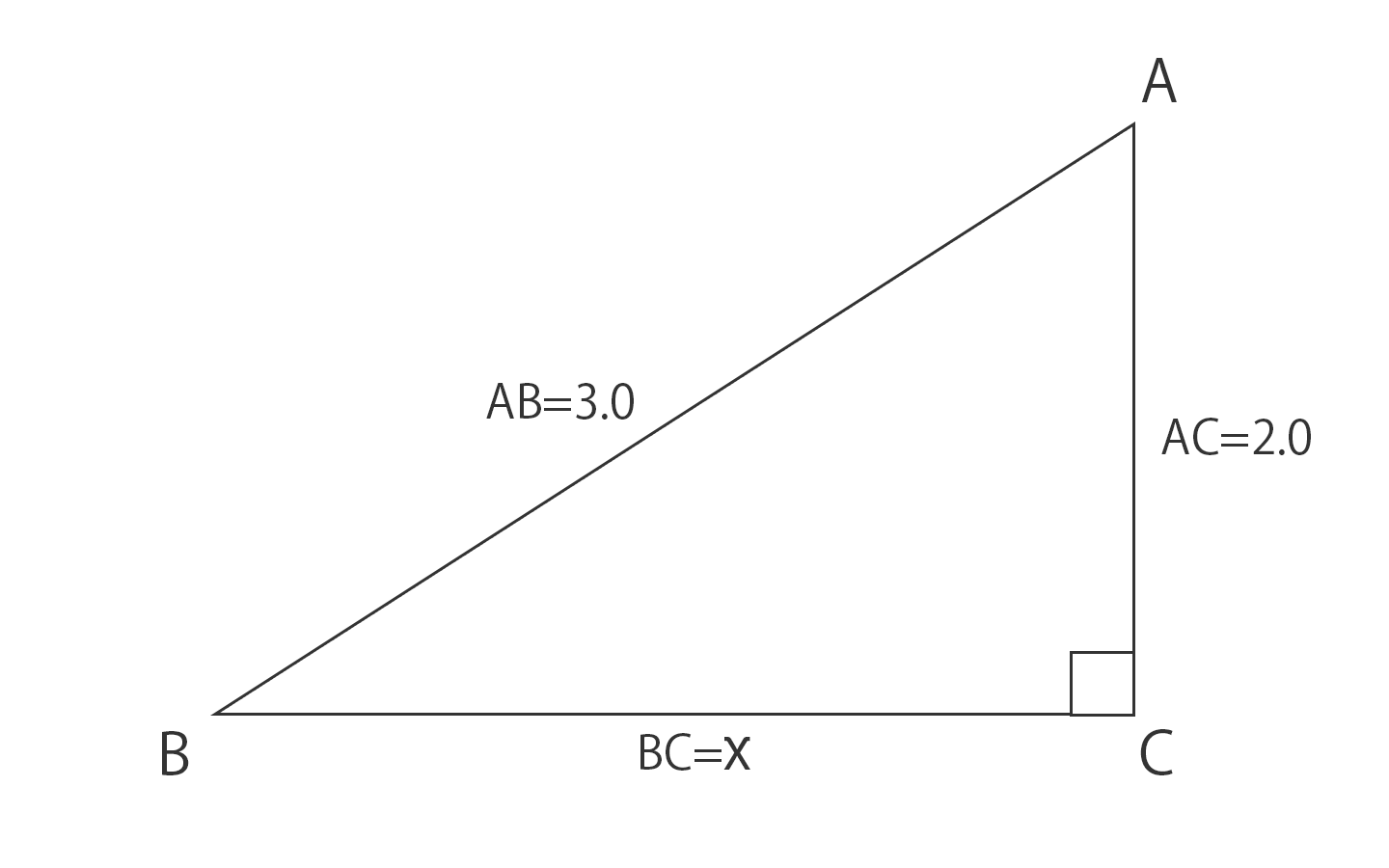



Python 三平方の定理 Unpyside
综上,我们得到直角三棱柱的"倒数面积勾股定理": 以直角三棱柱两两垂直的三条棱为长宽高的长方体,同上作出新长方体,则 上图中蓝色直角三角形的面积平方倒数 以直角三棱锥的三个直角面为其它三个直角三棱柱"倒数面积勾股定理"结果对应的直角Oct 30, 16 · 覚えて損はない!直角三角形の辺の比の3つのパターン 直角三角形の比は3つ覚えればいい?? こんにちは!ぺーたーだよ。 三平方の定理で覚えておきたいのは、 直角三角形の比 だよ。 これを覚えておけば、Oct 16, 17 · ①直角三角形的两个锐角互为余角; ②直角三角形斜边上的中线等于斜边的一半; ③直角三角形的两直角边的平方和等于斜边的平方(勾股定理); ④直角三角形中30度 角所对的直角边等于斜边的一半; 直角三角形的判定:




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
May 14, 21 · 1、勾股定理,直角三角形两直角边的平方和等于斜边的平方。 2、在直角三角形中,两个锐角互余。 3、直角三角形中,斜边上的中线等于斜边的一半,即为直角三角形斜边中线定理。 4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。Aug 11, 19 · 勾股定理直角三角形三边关系 141 勾股定理 勾股定理是我国最早证明 的几何定理之一,可以说是 a 中国几何学的根源,书本 p43页就是赵爽用来证明 勾股定理的弦图 b c三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 三平方の定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
Jun 22, 21 · >> 勾股定理直角三角形的两直角边的平方和等于斜边的平方 直角等腰三角形三边的关系是什么啊 ?>> 嗯,是很简单 2腰相等,底角为45°,√2(根号2)直角边=斜边 等腰直角三角形有哪些定理三边长关系,边长与高关系,等等许多 作业帮?>> a平方b平方=c平方三平方の定理直角三角形辺の長さ 四平方の定理直角三角錐面の面積 三平方の定理は, 直角三角形において,斜辺の平方は直角をはさむ2辺の平方の和に等しい と表現される. 四平方の定理を同様に表現すると,




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ



Q Tbn And9gcsnbiv 7svsm 6o0qjqco66pmarde4rrmbqkrgwufvawvziomrf Usqp Cau



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




三平方の定理の応用




2つの直角三角形の角の和 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




数学 中3 61 三平方の定理 基本編 Youtube




三平方の定理の証明 その3 Last Entry 第6話 Factory Takumaro ページ



三平方の定理



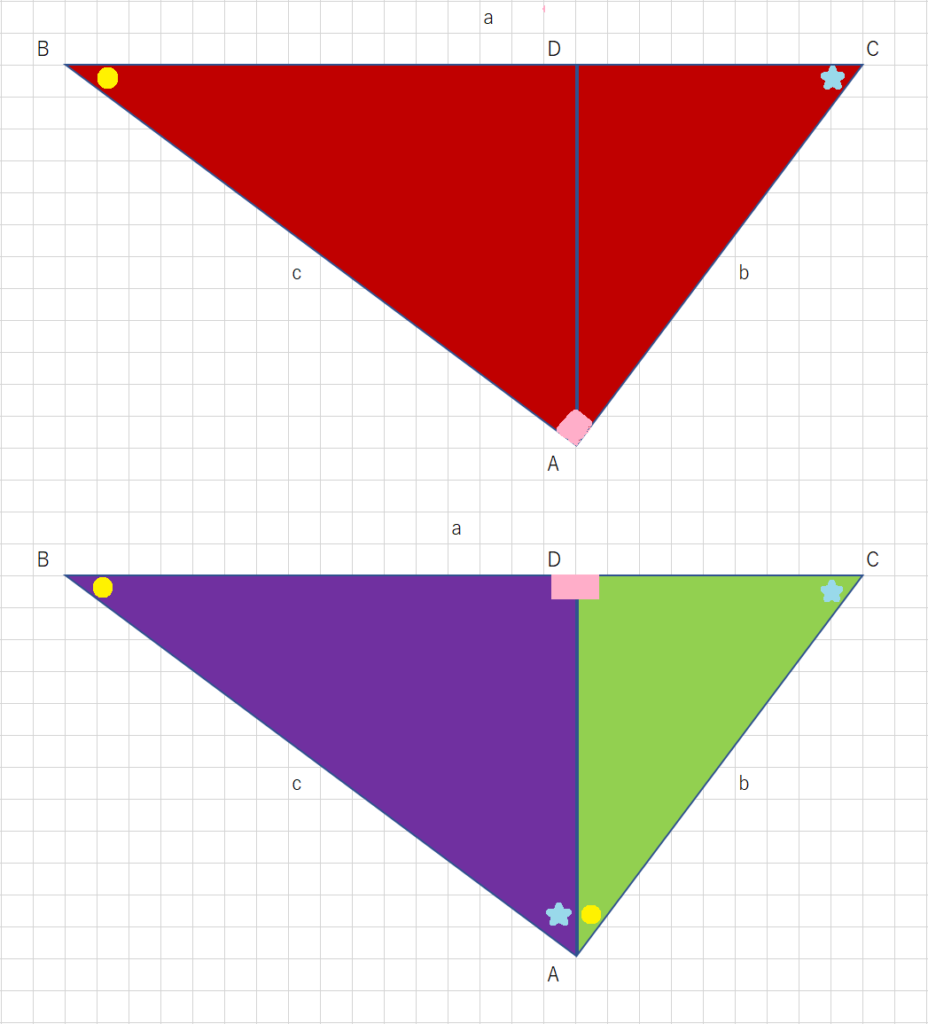
三角形のペア 大田 桐光本部校 ブログ




三平方の定理の導入 Geogebra




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



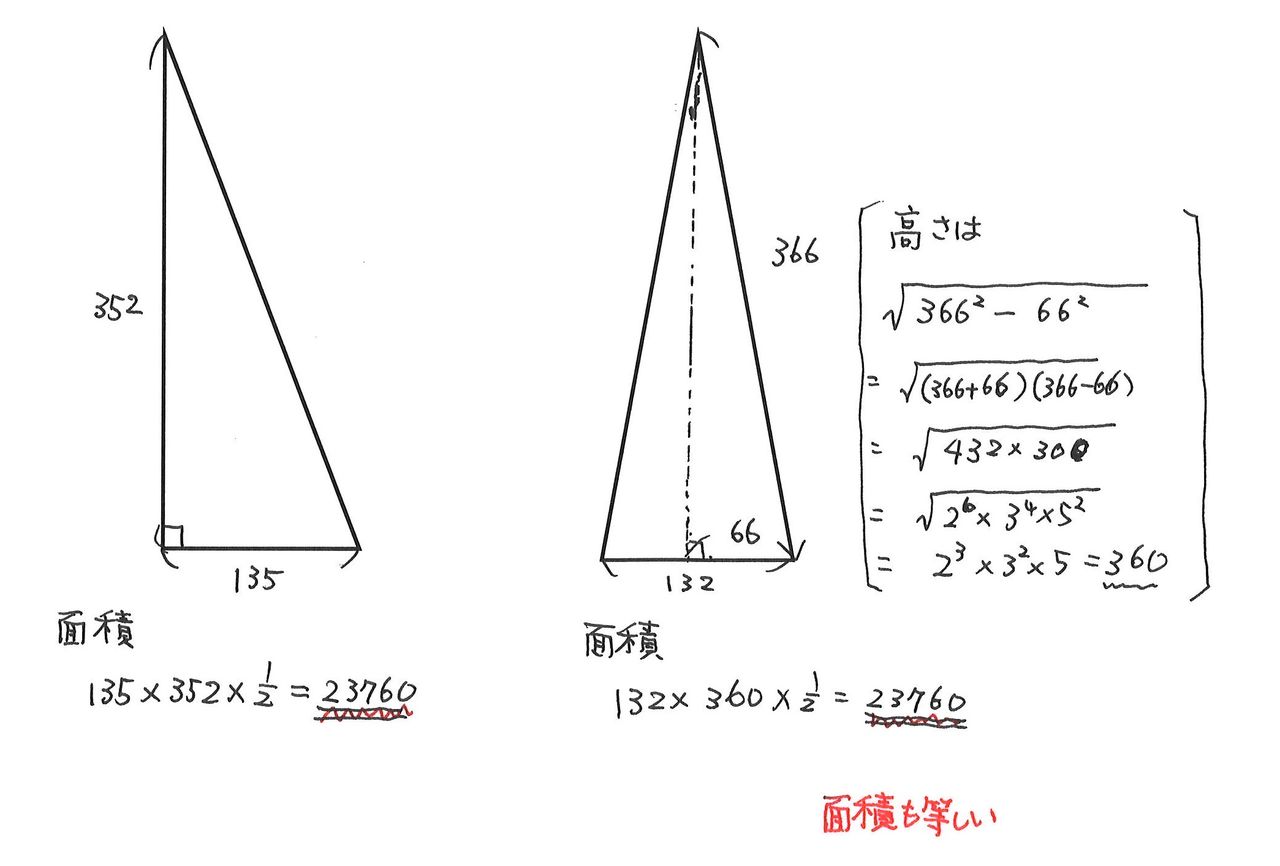
三平方の定理 をシミュレーションで復習しよう 数学入門



1




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に
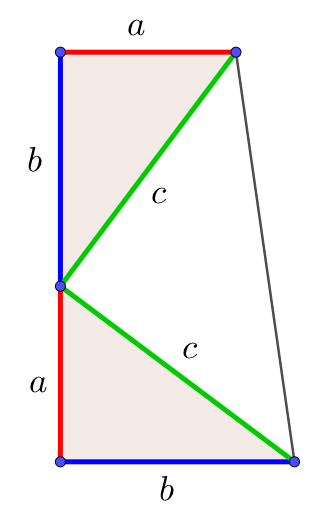



三平方の定理の証明3 大統領の台形 キソカラ



Python 三平方の定理 Unpyside



中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




直角三角形 Wikipedia




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく



三平方の定理 スタディーx




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学



3




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




勉強しよう数学 拡張三平方の定理




三平方の定理の証明と使い方




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典
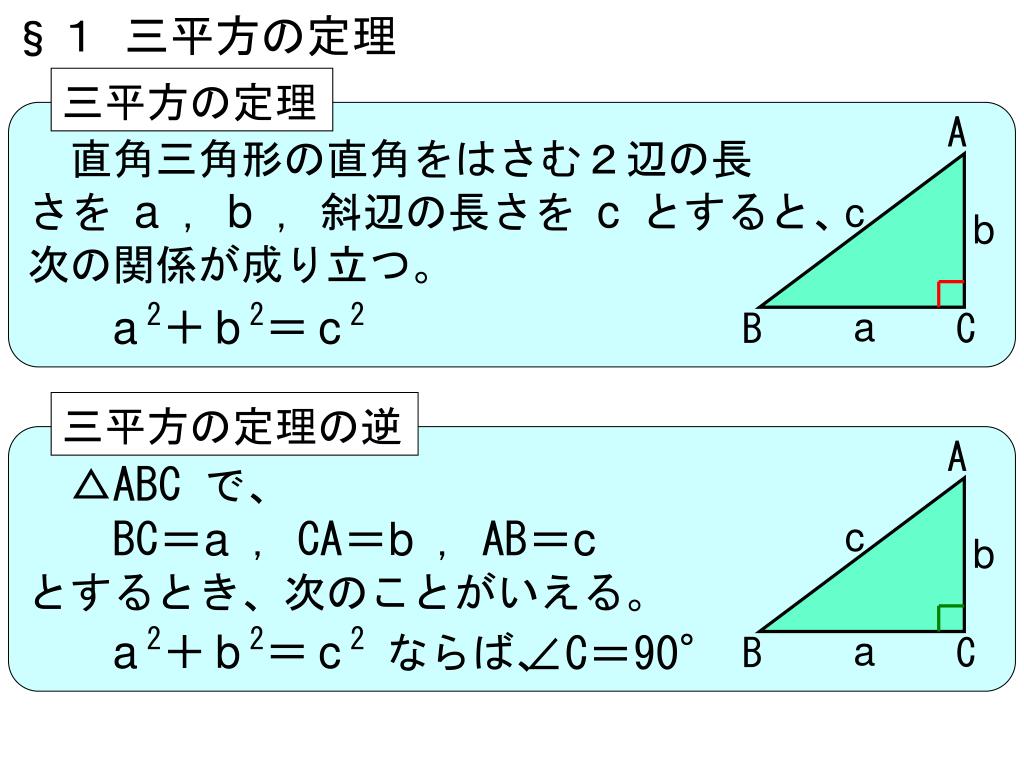



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id




なぜ 三平方の定理で角度bが90度だとわかるのですか Clear



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora



中学数学 直角三角形3 4 5以外に知ってる
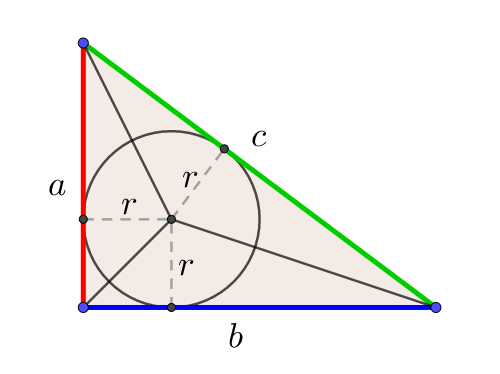



三平方の定理の証明4 直角三角形と内接円 キソカラ



三平方の定理




三平方の定理で3 4 5を習ってないのですが 簡潔に説明お願いします Clear



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




直角三角形



7章 三平方の定理 タカラゼミ




三平方の定理で辺を求める Youtube




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理の証明と使い方



三平方の定理の証明 直感的に分かる図で解説します 数学fun



1




三平方の定理を英語で読んでみる



高校入試対策数学 特別な直角三角形を使った問題 Pikuu



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




三平方の定理 自動計算サイト




三平方の定理を直角三角形二つで証明 Youtube



Documen Site Download Textbook T12 C01 Pdf




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
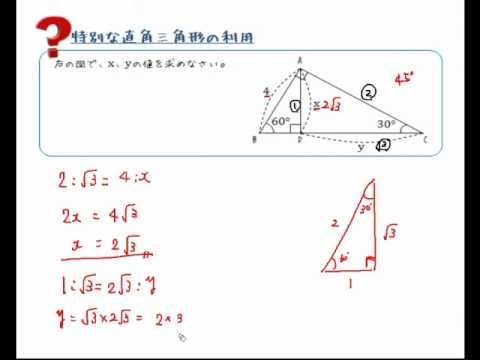



特別な直角三角形の利用 Youtube




三平方の定理 覚えておきたい基本公式を解説 数スタ




三平方の定理の証明と使い方




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理 ピタゴラスの定理




三平方の定理 特別な直角三角形 イ弋マ本ゼミナール




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




三平方の定理の証明 相似を利用した証明1 Fukusukeの数学めも




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




特別な直角三角形 Youtube




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理について考える5 直角三角形の合同条件のひとつ 身勝手な主張



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



Service Zkai Co Jp Jr Ikkanko Pdf Am3zy Pdf




X See How To Solve It At Qanda




正方形を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト




三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ



0 件のコメント:
コメントを投稿