二次関数の変化の割合を3秒以内に暗算で出す方法も証明し、解説しています。 (ご注意 このようなテクニックに関することは、本来は本質ビデオの意図に反していますが、 試験には制限時間があるため、やむを得ず、解説しました。変化の割合を、a(p+q) で表せば ⇒ =8 このように、あっという間に 「変化の割合」が求められます。 同じく、y=2x² で、 xが 「-3から-1まで」 増加するときの 変化の割合は ⇒ =-8 ほら、あっという間ですよね! ちなみに、今回のテーマは、「 変化の割合 」だよ。 1次関数y=ax+bにおいて、「変化の割合」が何を表すのか、先にポイントをおさえておこう。 POINT y=ax+bにおいて、「変化の割合」はa のことを指しているんだ。 つまり、 y= 2 x+1なら、 (変化の割合)=2 y= 5 x-4なら、 (変化の割合)=5 となるね。 まずはこれだけ覚えちゃおう。
二次関数についてです 二次関数は変化の割合が一定では無いのに Yahoo 知恵袋
2次関数 変化の割合 公式
2次関数 変化の割合 公式-変化の割合= yの増加量 xの増加量 比例反比例、1次関数、そして2乗に比例する関数、 変化の割合 はすべて同じ式を用いる。 ただし、1次関数では変化の割合は一定だが、 2乗に比例する関数では変化の割合は一定にならない。 y=3x2 についてそれぞれの場合の変化の割合をもとめる。 xが−3から1まで変化するとき xが1から5まで変化するとき ① xが3から1まで変化する2次関数 復習をしておきましょう。 場合分け をして考えるのが一般的です。 最大値はありません。 また,原点まで変化の割合が負の減少関数であったものが, 含まれる場合には,最小値は に なります。 最小値はありません。 また,原点まで変化の




1次関数の公式 変化の割合の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
中3数学 2次関数 変化の割合⑤ 今回の問題はこちら 関数 y =ax^2 と y=3x2 は、 x が ー2から6まで増加するときの変化の割合が等しくなる。二次関数 変化の割合 2次関数の変化の割合 名前 1.関数 32について,xの値が次のように増加するときの 変化の割合を求めなさい。 (1)4から7まで (2)からまで 2.関数 2について,xの値が次のように増加するときの 変化の割合を求めなさい。 (1)4から5まで 2次関数変化の割合簡単な求め方 21年2月1日 学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとうございま
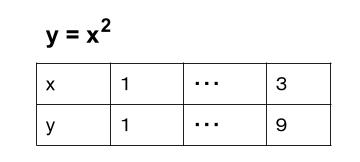
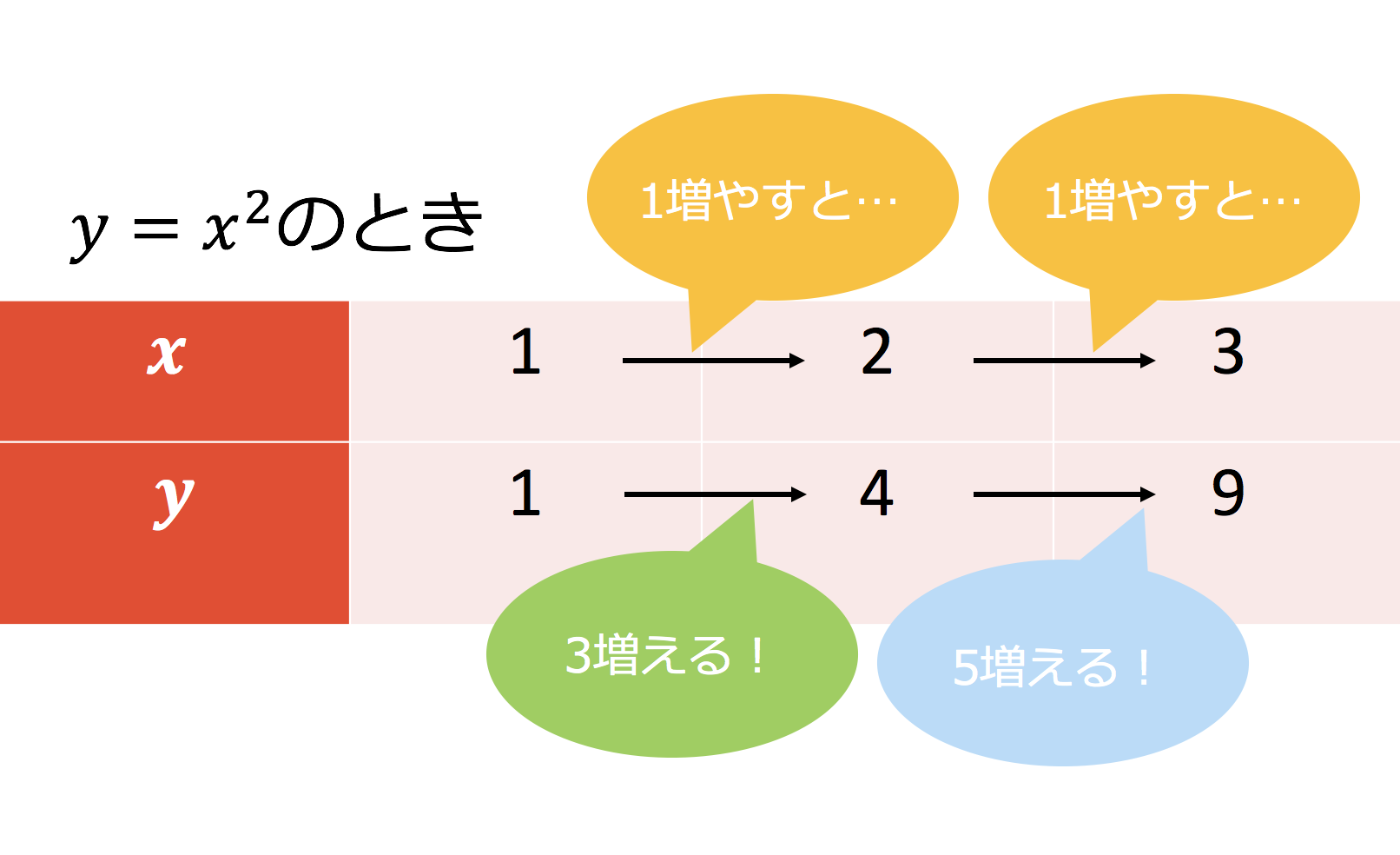
今日はy=ax 2 における「変化の割合」を求める問題をやるよ。 「変化の割合」は、1次関数y=ax+bのときにはxの係数であるaの値で一定だったね。 一次関数では変化の割合とa(比例定数)は同じですが 二次関数のaはただの比例定数です 比例定数というのは、yやxによって左右されない数字 一次関数では、どの2点で結んでも直線上にあるため、グラフ自体の傾きは常に一定です そのため、変化の割合(傾き)が変わることがなく、比例 中学2年生数学ー1次関数(変化の割合) 1 次関数の変化の割合について学習するよ。 先生、変化の割合ってなんですか? 変化の割合とは、ある関数において、yの増加量/xの増加量で求められる値のことをいいます。 確かに言葉だけだと難しいよね。 次
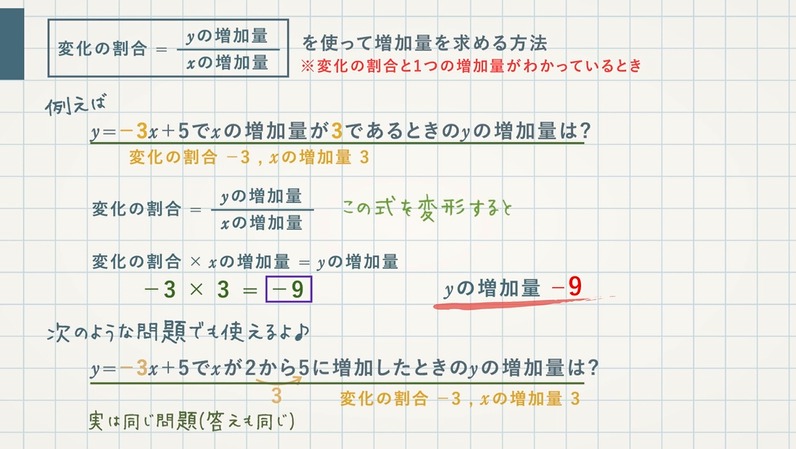
次の問いに答えよ。 1次関数で xが5から8まで変化したときにyは7から13まで変化した。 変化の割合を求めよ。 1次関数でxが5から6まで変化するときにyが9から7まで変化した。 変化の割合を求めよ。 y=-2x11について 変化の割合を求めよ。 xが3増加するときのyの増加量を求めよ。 y= 3 2 x-8について 変化の割合を求めよ。変化の割合 = yの増加量 xの増加量 だから、 関数 y=ax 2 はxがどの値からどの値まで増加するか によって変化の割合は異なってくる。2次関数のコツ、成績アップ法を公開。 2乗に比例する関数 ( y = ax² ) の「変化の割合」とは? 中3生の「数学」のコツ




二次関数とグラフ 数学の要点まとめ 練習問題一覧




数学教材 ページ 9 数学教材
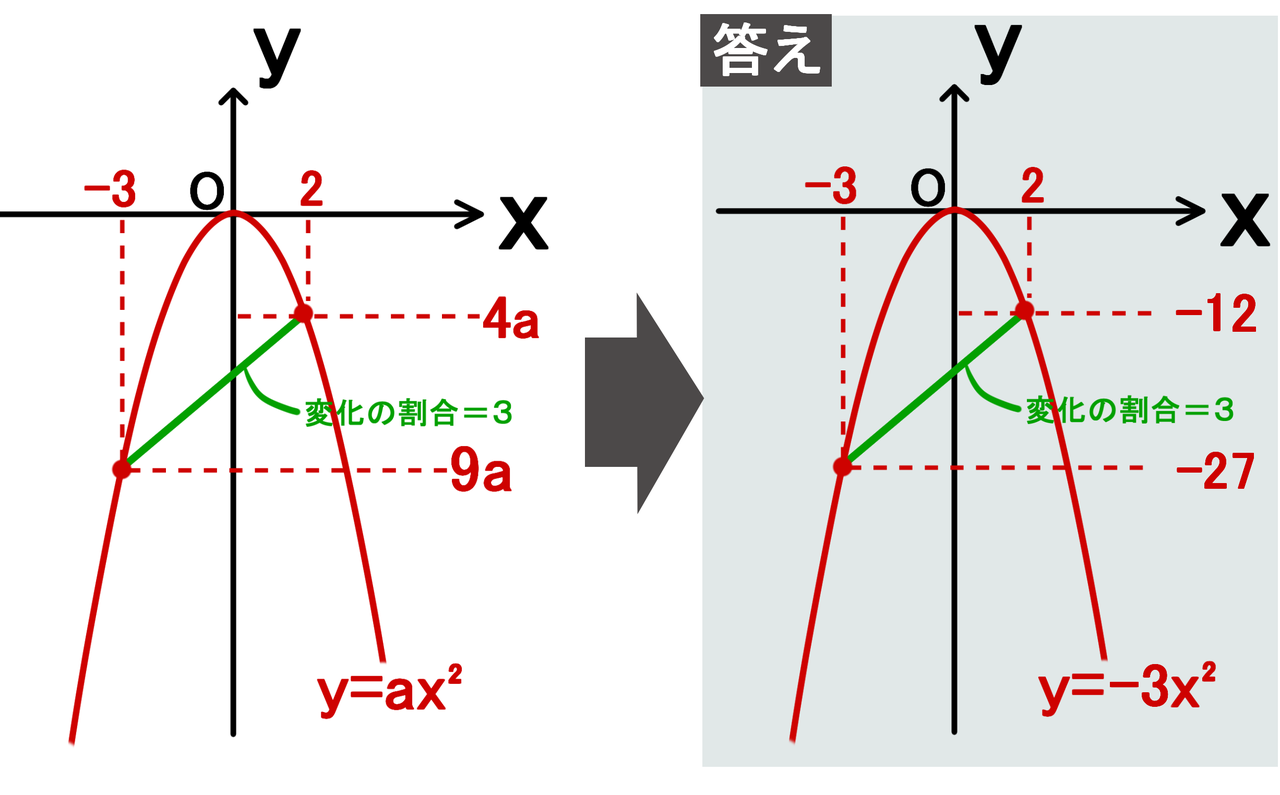
次関数の変化をグラフにより比較することで、1次 関数の変化の特徴をつかむ。また1あたりの変化量 である変化の割合を1次関数と2次関数を比較し ながら定義する。 2 1次関数の性質 ・水そうの問題 ・変化の割合 2 ・はじめから水が入っている水そうに一定Sway is an easytouse digital storytelling app for creating interactive reports, presentations, personal stories and more Its builtin design engine helps you create professional designs in minutes With Sway, your images, text, videos, and other multimedia all flow together in a way that enhances your story Sway makes sure your creations look great on any screen(2)(1)を用いて,関数 のxの値が4から2まで増加するときの変化の割合を求めなさい。 解説・解法 y=ax 2 の変化の割合の中でも少し応用編というか,発展編です。教科書には載っていませんが,この公式を覚えておいたら楽に点数が取れます。



1次関数の値の変化 増加量と変化の割合 教遊者




1次関数の値の変化 増加量と変化の割合 教遊者
2次関数の変化の割合2 名前 1.関数 2で,xの値が から に変化するとき の変化の割合が ( )になることを証明します。 ( )にあてはまる記号や数を答えなさい。 の増加量( ) ( ) の増加量 ( )2 ( )2 の増加量 ( )2 ( )2 の増加量 ( ) ( ) {( )2 ( )2}「変化の割合=(y の増加量)/(x の増加量)」で求めることができるので、こちらの式に代入します。 質問内容を確認しますと、こちらの式に使われる「増加量」の求め方が正しくないようですね。1次関数(変化の割合) 変化の割合= yの増加量 xの増加量 について( )に適切な数字を入れよ。 x が3増加するときに y が15増加する。 これを変化の割合の式にあてはめると 変化の割合= ( ① ) 3 =( ② ) 座標上に点A(1, 3)と点B(6, 23)があり、点Aから点Bへ変化するとき。




世界一わかりやすい数学問題集中3 4章 二次関数



8月23日の授業日記 中3一斉授業 2次関数の変化の割合 裏ワザあり 成績 上がってます 根城学習塾 八戸市
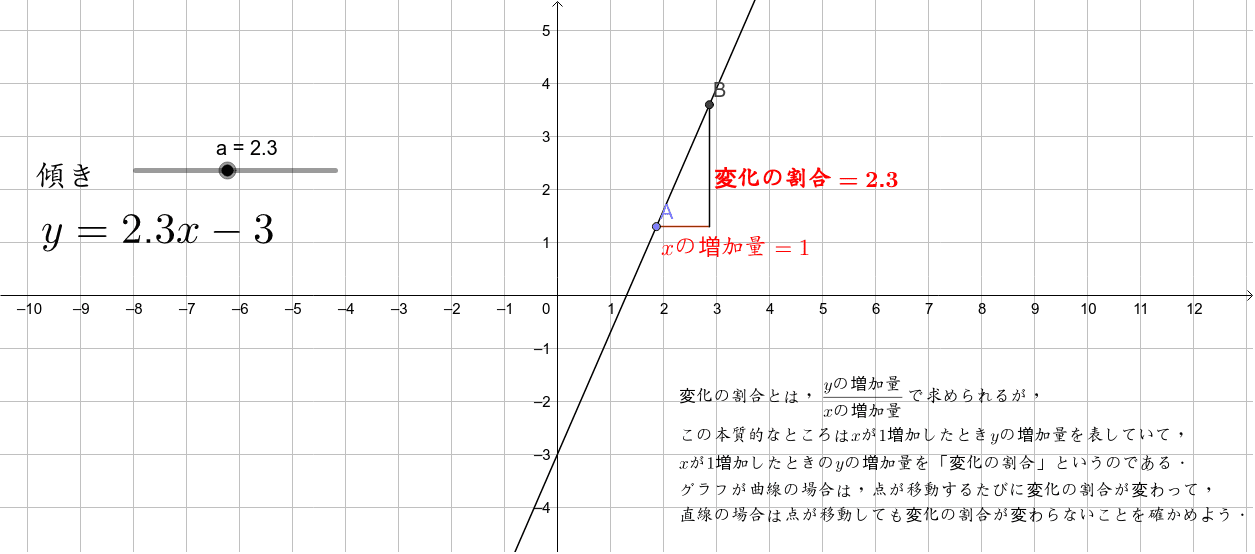
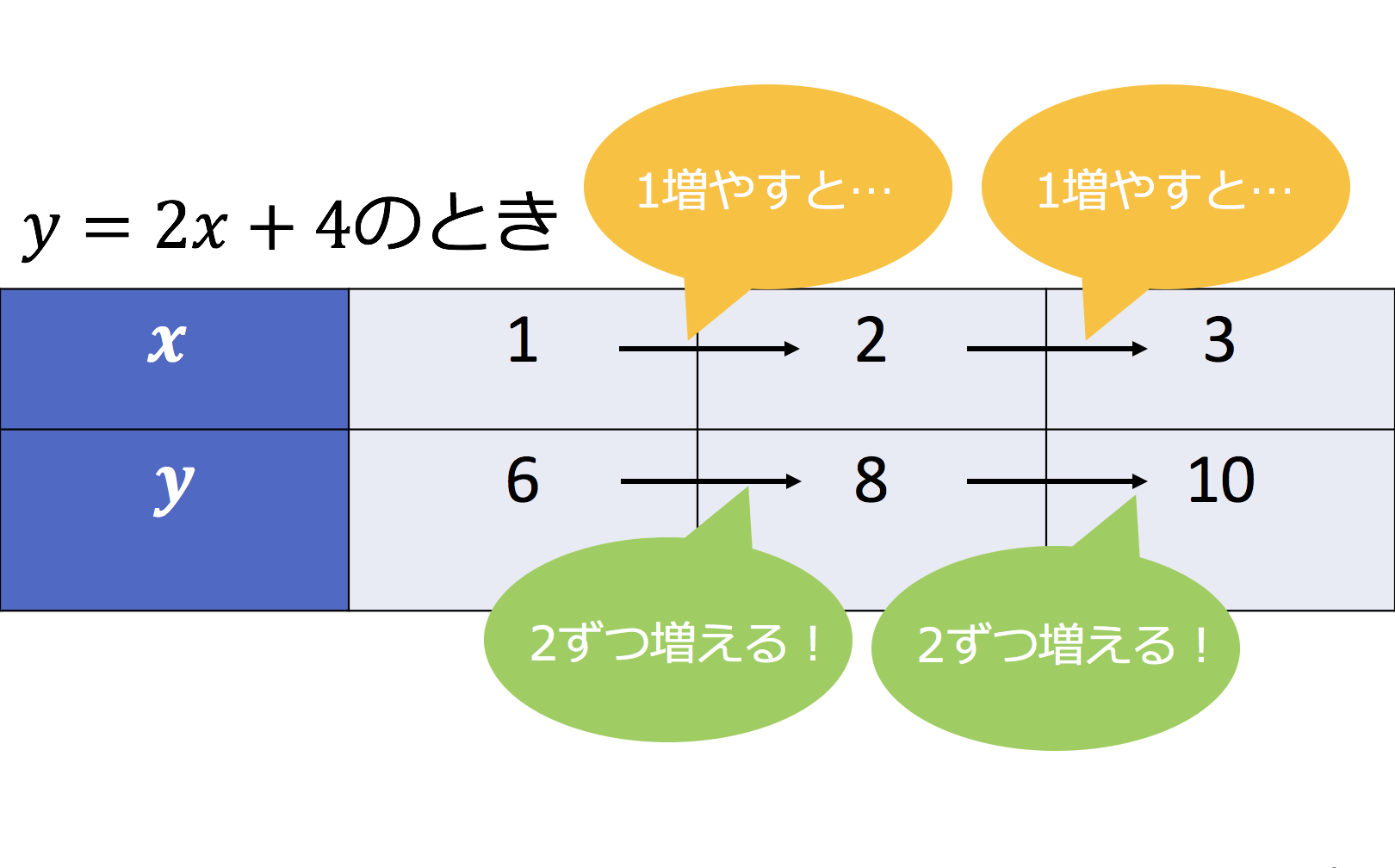
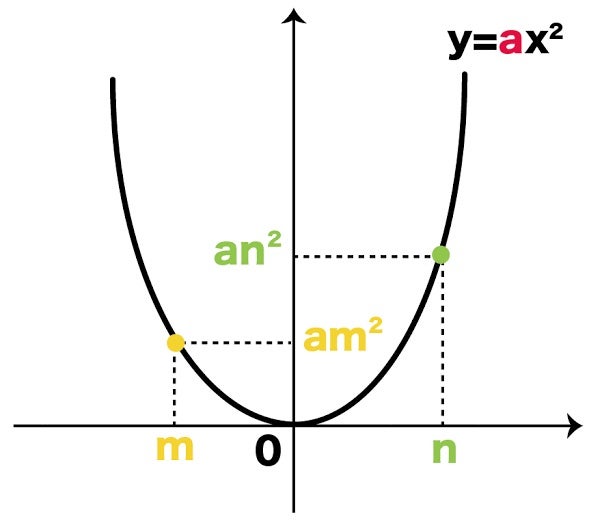
Point ① y がxの関数であるとき、この関数の (変化の割合) は、 次の式で求めることができる。 (の増加量) (の増加量) (変化の割合)= x y ② 1次関数y =ax b の変化の割合は(一定)であるが、表やグラフからわかるように、 2次関数 y =ax2 の変化の割合は(一定ではない)。関数 \(y=ax^2\)について、\(x\)の値が\(m\)から\(n\)まで増加したときの変化の割合を考える。 基本形の解き方通りに考えてみると 表はこのようになります。で定義されており, 「 変化の割合 」は になります. 他の例として,次の関数 y=−x3 (図2)においては, x が 0 から 3 まで変化するとき( x は 3 増加), y は 3 から 0 まで変化します( y は 3 減少) 図2 x の増加量 = ( x の最後の値)- ( x の最初の値) = 3−0=3 です. y の増加量



二次関数についてです 二次関数は変化の割合が一定では無いのに Yahoo 知恵袋



1次関数 反比例 2次関数の変化の割合 Geogebra
This is "7月13日(火)2次関数 変化の割合" by original on Vimeo, the home for high quality videos and the people who love them よって、 二次関数においても変化の割合は\(x\)を変化させる場所によって変わる ことが確認できました。 二次関数における変化の割合も二次関数の一般式\(y=ax^2bxc(a \neq 0)\)の\(a\)とは常に一致しないことに注意です。二次関数 ( )の変化の割合は が から まで増加するとき 変化の割合簡単な求め方は? まとめ! 一次関数、二次関数においては今回紹介したように簡単に求める方法がありました。 しかし、反比例などの関数においては基本通りにそれぞれの増加量を




中3数学 Y Ax 2の変化の割合 例題編 映像授業のtry It トライイット




二次関数の変化の割合の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
Sway is an easytouse digital storytelling app for creating interactive reports, presentations, personal stories and more Its builtin design engine helps you create professional designs in minutes With Sway, your images, text, videos, and other multimedia all flow together in a way that enhances your story Sway makes sure your creations look great on any screen中学2年 数学 式の計算 式の計算 練習問題 単項式・多項式;変化の割合(2次関数) 問題 「関数y=-2x^2について、xの値が1から3まで増加するときの 変化の割合を求めなさい。」 2次関数の基本的な問題のうちのひとつですね。 重要 数式は以下のルールに従って書いています。




変化の割合の求め方 一次関数と二次関数の変化の割合を求めよう 中学や高校の数学の計算問題



1
よって,求める 次関数の式は \ ③ \ 切片は である。 グラフの傾きは である。 よって,求める 次関数の式は \ 2 変化の割合が であるから,求める 次関数の式は \ e とおける。 のとき \ であるから e2次関数 練習問題 2次関数 比例定数aを求める;<2 次関数 変化の割合・変域 練習問題> No 2 変化の割合 (1) 関数у =-χ 2 で、χ の値が次のように変化する場合の変化の割合を求めよ。 ① 0から2まで ↙ それぞれ増加か減少か、よく見てね。 代入した後の計算注意!




2次関数 変化の割合 清水塾



中学数学 Y Ax 2 変化の割合の意味 中学数学の無料オンライン学習サイトchu Su
2次方程式 練習問題 2次方程式の利用 図形;変化の割合のポイントは! 変化の割合とは、x の増える量に対して、y がどれだけ増えたかを示す割合で、( y の増加量 ) / ( x の増加量) で求める1 1 次関数のときにもでてきた変化の割合です。 定義を覚えていますか? です。 でした。 変化の割合は常に一定であり、ただの「 a a 」 や「傾き」の別名でしかなかったものです。 2 2 乗に比例の y = ax2 y = a x 2 においては、変化の割合は一定ではあり



2次関数 変化の割合 中学から数学だいすき



3分で分かる 変化の割合とは 意味やその求め方など 合格サプリ
2次関数の変化の割合とは? 復習になりますが、変化の割合とは \(x\)に対して\(y\)がどれだけ変化するかを表す値 です。 「\(x\)が1増えた時の\(y\)の増加量」、具体的には「\(\dfrac{yの増加量}{xの増加量}\)」です。 1次関数の場合、変化の割合は常に一定なので、『傾き=変化の割合』でした。




2次関数 膨大なページ数 Wiki




Mathematics 2次関数 2乗に比例 の 変化の割合 を簡単に求める方法 働きアリ




中3数学 二次関数 𝑦 𝑎𝑥 と 𝑦 3𝑥 の変化の割合が等しくなるときの 𝑎 の値 Youtube




二次関数のグラフでは変化の割合が一定ではないと思うのですが 写真のように求めているa Clear




1次関数の表から変化の割合 Geogebra




3分で分かる 変化の割合とは 意味やその求め方など 合格サプリ




Y Ax2乗の利用 平均の速さの求め方は変化の割合と同じだ 中学数学 理科の学習まとめサイト




変化の割合を求める 1次関数 あんず学習塾のメモ 図表置き場




中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学
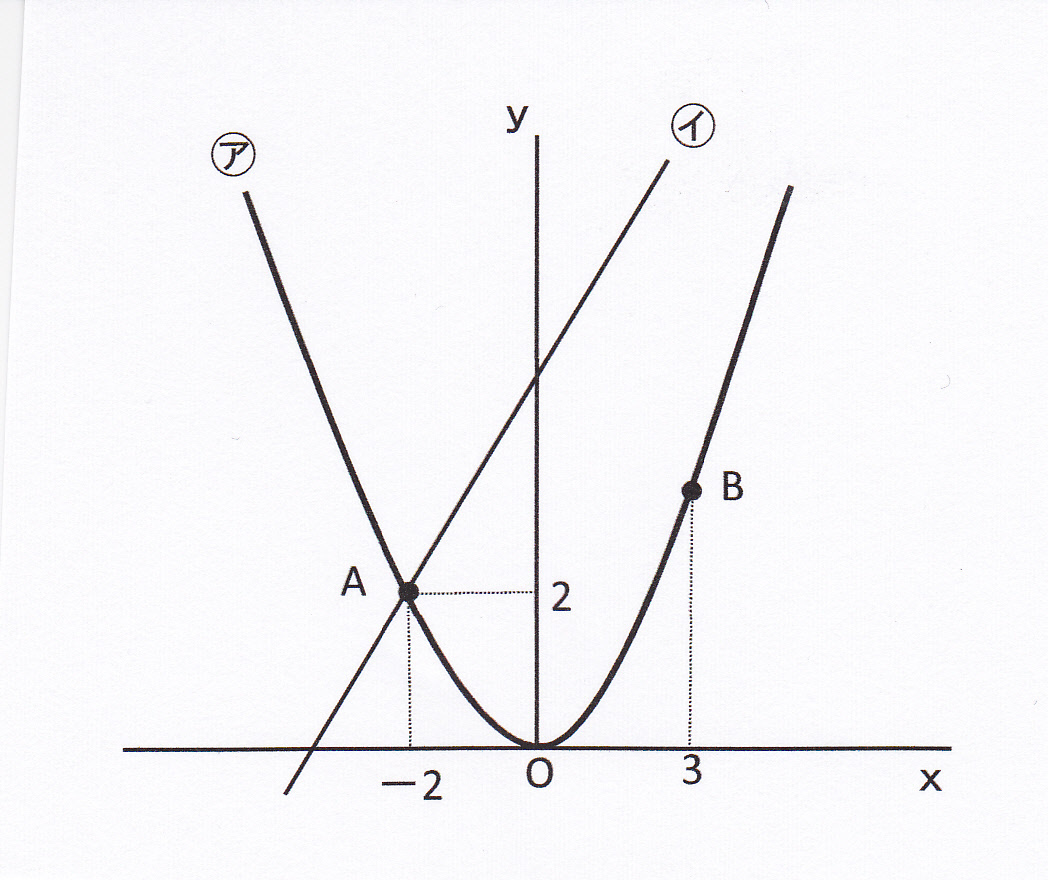



二次関数と一次関数の融合問題の解き方 座標 変化の割合 など 現役塾講師のわかりやすい中学数学の解き方




中3数学 二次関数9 変化の割合 すべて無料 星組の中学数学講座




二次関数の変化の割合の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
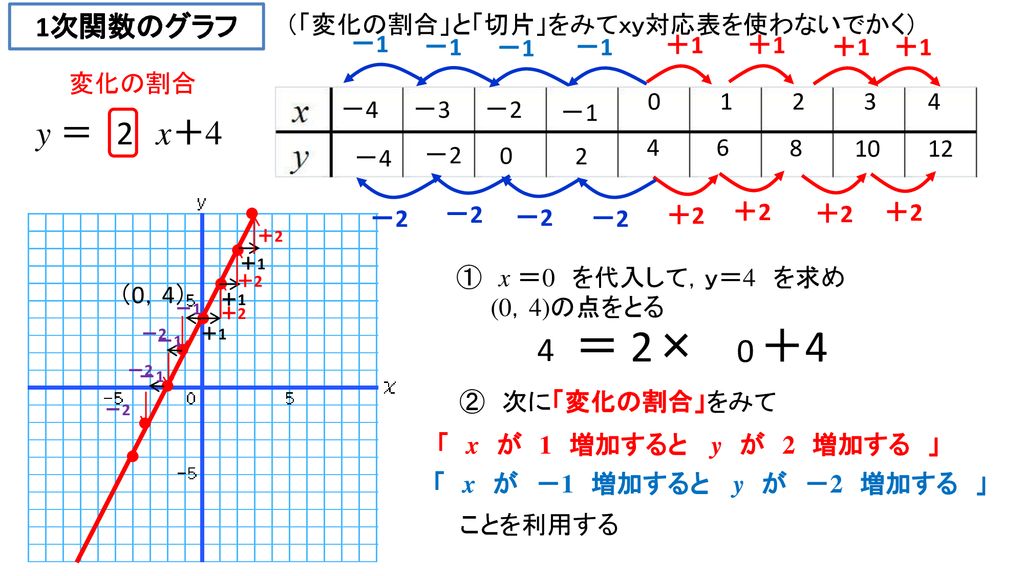



1次関数のグラフ テーマ 目的 xyの対応表を使って 考えられるすべての点をうってグラフをかく以外に 変化の割合を使ってグラフをかく Ppt Download




1次関数の変化の割合の導入 Youtube




2次関数の変化の割合の問題の解き方 ポイントを解説 数学fun




数学 時短演習cote
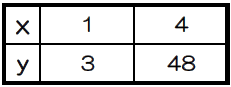



2次関数 変化の割合 簡単な求め方 学習内容解説ブログ




変化の割合 無料で使える中学学習プリント



また中3の数学についての質問です これもテストによく出るのですが Yahoo 知恵袋




1次関数の変化の割合 Youtube




1次関数の公式 変化の割合の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中3数学 二次関数10 変化の割合 A P Q すべて無料 星組の中学数学講座



U9j580gf8iba369ji2w Xyz P 762




2次関数と変化の割合 基 標 数学の解説と練習問題



中学3年生 数学 2次関数 変化の割合 On Vimeo
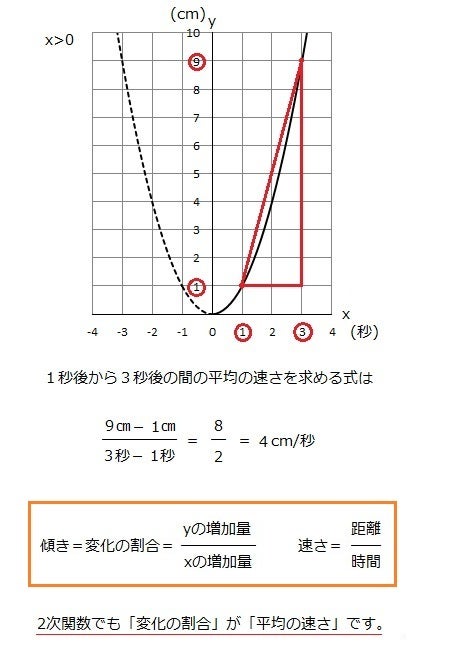



平均の速さは変化の割合 傾き 永和進学ゼミ 個別指導ソフィア 学習塾ブログ
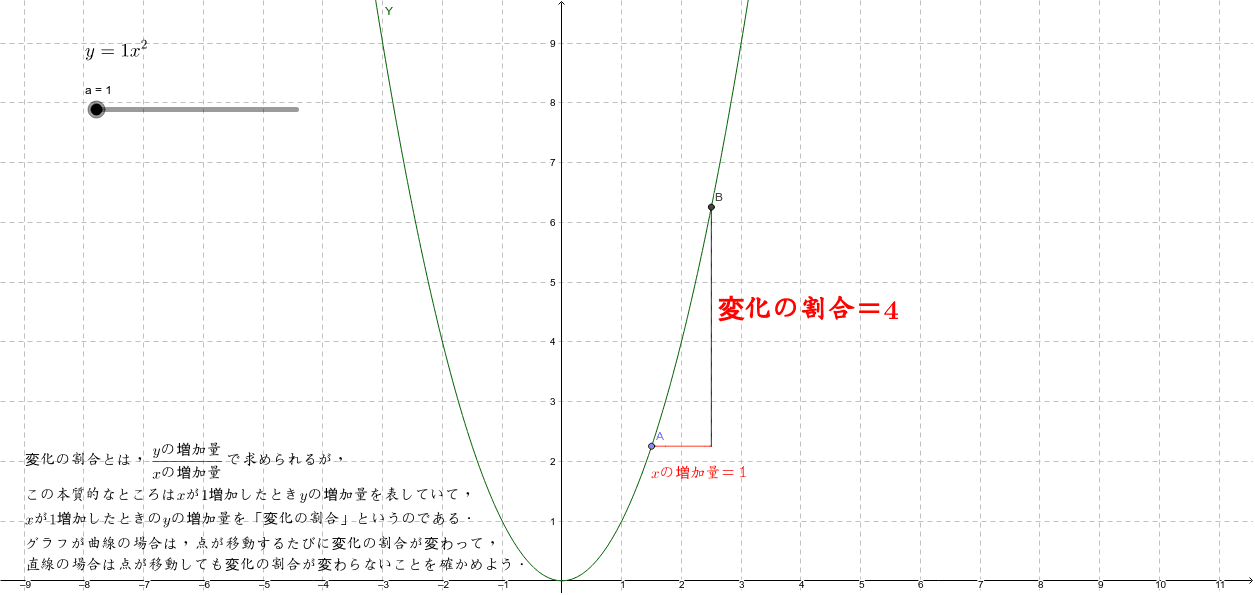



1次関数 反比例 2次関数の変化の割合 Geogebra




変化の割合




二次関数の変化の割合の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
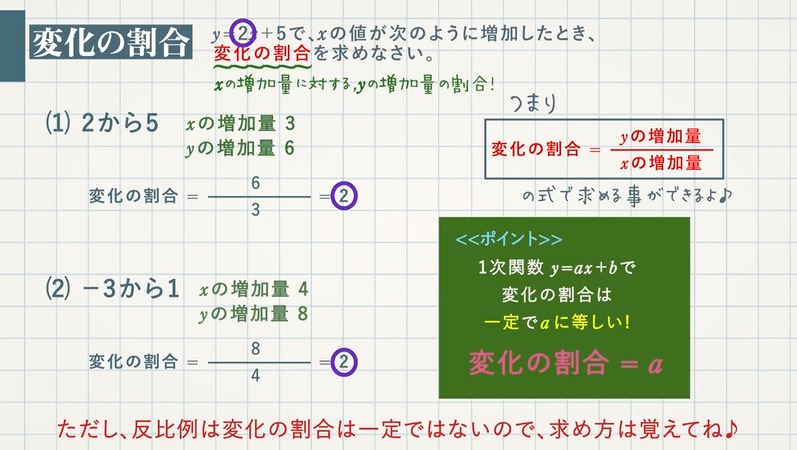



1次関数の値の変化 増加量と変化の割合 教遊者



二次関数とは 平方完成の公式や最大値 最小値 決定の問題 受験辞典




中学3年の数学 動画 二次関数の変化の割合の問題 19ch
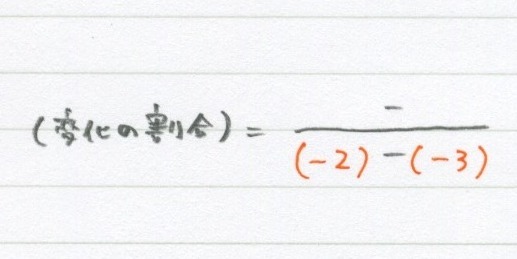



10 3 2次関数 変化の割合 勉強できようサイト




中2数学 変化の割合 映像授業のtry It トライイット




変化の割合 Xの変化量分のyの変化量 を使えるのって二次関数の時だけですか Clear



8月23日の授業日記 中3一斉授業 2次関数の変化の割合 裏ワザあり 成績 上がってます 根城学習塾 八戸市



Y Ax 2の変化の割合は一定じゃないんですか Aが変化の割合であって Yahoo 知恵袋




中学3年数学 変化の割合の計算 交点の座標 練習問題1 あんのん塾




変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ




2次関数 変化の割合 簡単な求め方 学習内容解説ブログ




変化の割合 清水塾




1 1 X 2 Y1 1 12 Descubre Como Resolverlo En Qanda




傾きと切片の意味と求め方を丁寧に解説 具体例で学ぶ数学



写真ような場合なぜ一次関数は問題の8が変化の割合として扱えるのに二次関数は 1 Yahoo 知恵袋




変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ




数学 中学3年生 二次関数の変化の割合 傾き の求め方のコツ なるほど 塾講師が教える教え方のコツ




1次関数 変化の割合 清水塾



1次関数の値の変化 増加量と変化の割合 教遊者




10 3 2次関数 変化の割合 勉強できようサイト



二次関数の変化の割合の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




y ax2の変化の割合の求め方 基本と裏ワザ 現役塾講師のわかりやすい中学数学の解き方




中3 数学 平均の速さの求め方を解説 数スタ




1 4 Times4 1 Descubre Como Resolverlo En Qanda




1次関数の値の変化 増加量と変化の割合 教遊者
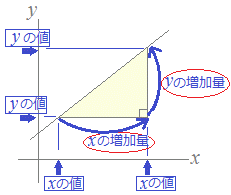



変化の割合
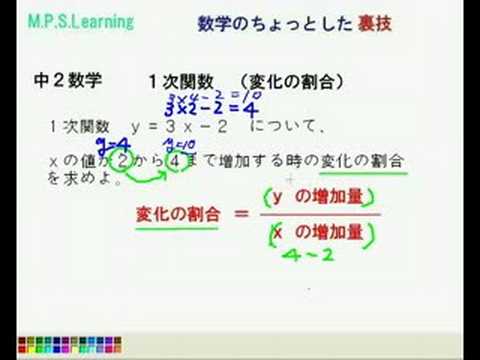



中2数学 1次関数 変化の割合 Youtube




数学 中2 29 変化の割合 Youtube
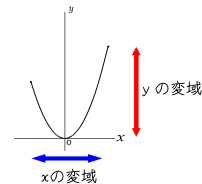



2乗に比例する関数 変域 変化の割合




一次関数 一瞬で答えられる変化の割合 苦手な数学を簡単に
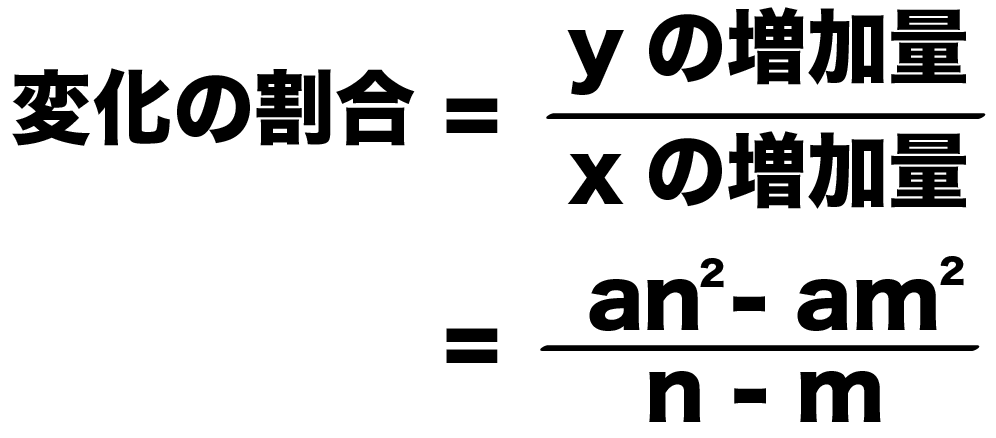



二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



開成ハイスクールブログ ブログアーカイブ 2次関数から微分 積分へ



関数とは 意味や用語 切片 変化の割合 傾き を簡単に解説 受験辞典




中2数学 変化の割合 映像授業のtry It トライイット



3分で分かる 変化の割合とは 意味やその求め方など 合格サプリ




3分で分かる 変化の割合とは 意味やその求め方など 合格サプリ




2次関数 変化の割合 Youtube



関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学
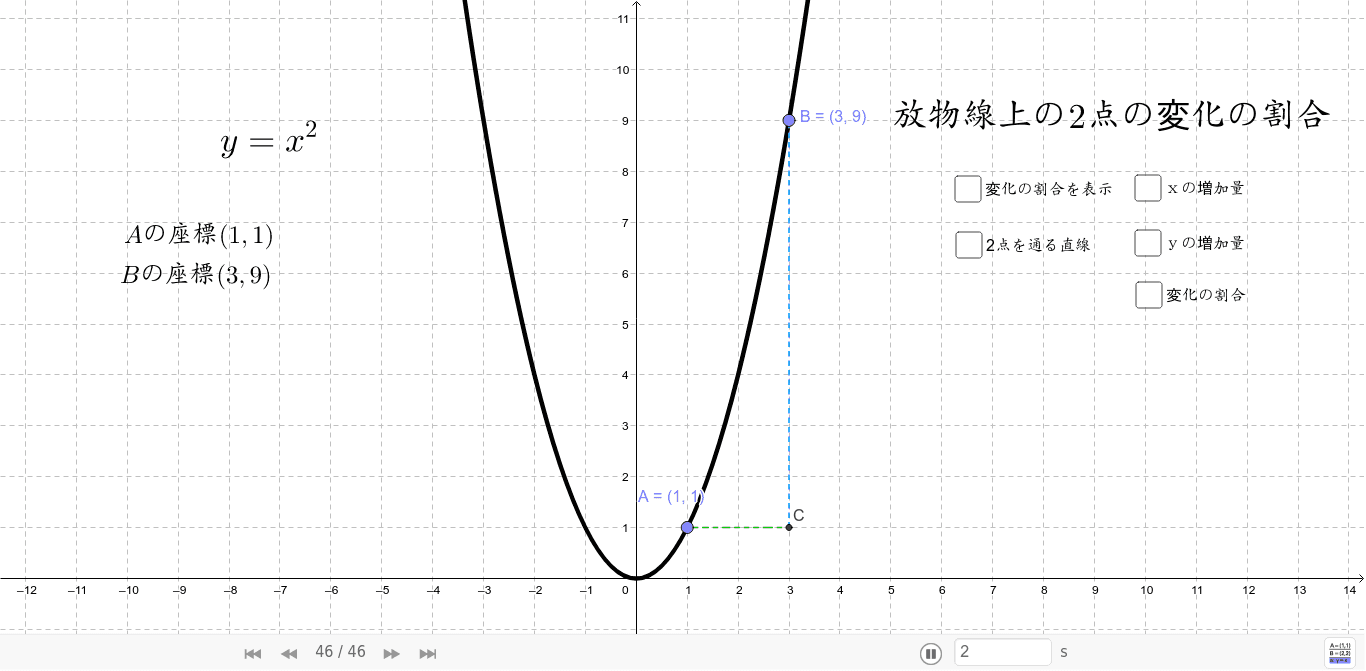



二次関数の変化の割合 Geogebra




二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場



1




10 3 2次関数 変化の割合 勉強できようサイト




2乗に比例する関数 変化の割合 無料で使える中学学習プリント




2 1 3 1 Descubre Como Resolverlo En Qanda




変化の割合とaの値の違いってなんですか Clear



二次関数の変化の割合 人生賭けた学習塾 松塾 第12期




これどうやって解くんですか 丁寧に教えてください Clear




平均の速さは変化の割合 傾き 永和進学ゼミ 個別指導ソフィア 学習塾ブログ




中2数学 1次関数の変化の割合の求め方と練習問題



Mathematics 2次関数 2乗に比例 の 変化の割合 を簡単に求める方法 働きアリ The 2nd
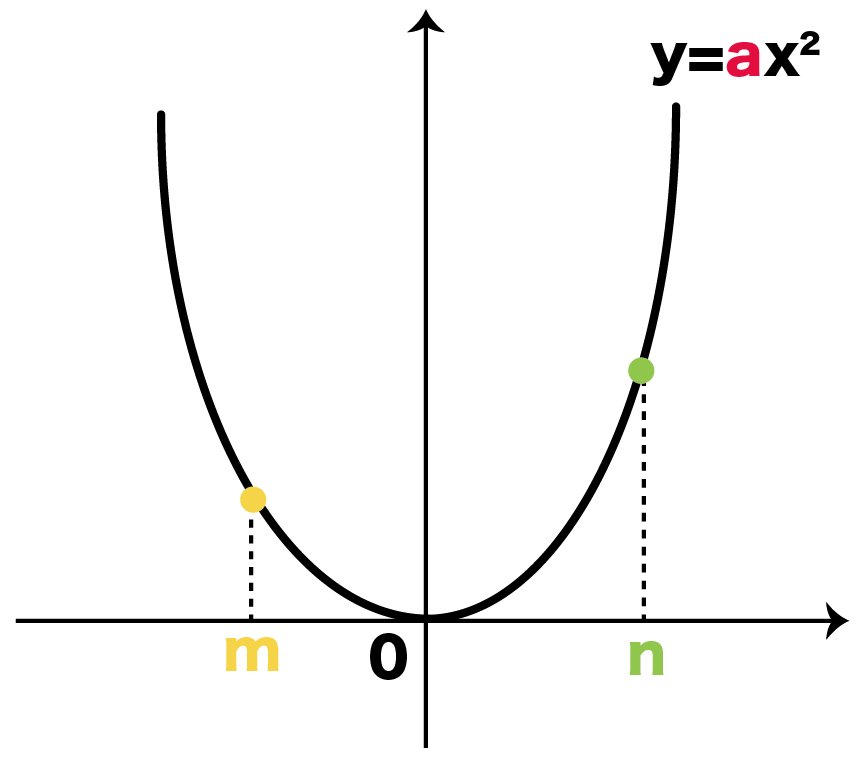



二次関数y Ax2の変化の割合を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
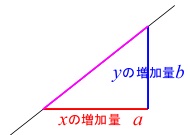



変化の割合とは 1次関数の求め方と直線の方程式との違い



1




数学 学校では教えてくれない1次関数の裏技 中学生 数学のノート Clear



変化の割合とは 1分でわかる意味 公式 傾きと増加量との関係



1次関数 板書




数学 中3 38 二次関数の変化の割合 Youtube



3



0 件のコメント:
コメントを投稿