Y = x 2 5x 3;The Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5From the equation of a parabola identify the focus and directrix (y3)^2=12(x1) From the equation of a parabola identify the focus and directrix (y3)^2=12(x1) Categories English Leave a Reply Cancel reply Your email address will not be published Required fields are marked *

The Distance Between The Vertex Of The Parabola Y X 2 4x 3 And The Centre Of The Circle X 2 9 Y 3 2 Is
Graph the parabola y=(x+3)^2-4
Graph the parabola y=(x+3)^2-4-The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, and the vertex is (0, 3) Observe the graph of y = x 2 3 Hence, intersection point is C(5, 3) and other points are A(0, 3), B(0, – 1) From the figure, we can see that, By taking a horizontal strip The area under shaded portion = Area under parabola from y = – 1 to y = 3 Tip Take limits as per strips If strip is horizontal than take y limits or if integrating concerning y then limits are of



Vertex And Intercepts
Correct answer Y = (x 2)2 3 Identify the vertex of the parabola The area (in sq units) bounded by the parabola y = x^2 1, the tangent at the point (2, 3) to it and the yaxis asked in Mathematics by Simrank (Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = − 1, b = − 4, c = − 3 a = 1, b = 4, c = 3 Consider the vertex form of a parabola a ( x d) 2 e a ( x d) 2 e Substitute the values of a a and b b into the formula d = b 2 a d = b 2 a
What is the following parabola's axis of symmetry of $$ y =x^2 2x 3 $$ Answer Since this equation is in standard form, use the formula for standard form equation $$ x = \frac{ b}{ 2a} $$ Answer the axis of symmetry is the line $$ x = 1 $$ Problem 7 What is the following parabolaCorrect answers 1 🔴 question (y3)^2=3(x3)/2 to general form of parabolaNotice, Solving the equation of straight line y = k x − 1 & equation of the parabola y = x 2 3 k x − 1 = x 2 3 x 2 − k x 4 = 0 Now, the line will touch the parabola if both real roots of the above
If y=2 x3 is a tangent to the parabola y^{2}=4 a\left(x\frac{1}{3}\right), then 3(a5) is equal toSolution for Graph the vertical parabola for y = 2(x – 4)² – 3 %3DY = 5x 12 y = x^2 2x 3 3x^5 6x^3 4x 12 y = 2 ⋅ 3^x eeduanswerscom



Instructional Unit The Parabola Day 4 And 5



Solution Graph Y X 2 3 And Y X 3 2 What Are The Similarities And Differences Between The Graphs How Do These Graphs Compare To The Graph Of Y X 2
En parabelkurva kan även fås som ett kägelsnitt och därmed en andragradskurva Parabeln är en av de elliptiska funktionerna En parabel med lodrät symmetrilinje och vertex i origo kan beskrivas med en andragradsfunktion y = x2 /4 a, där a är avståndet från vertex till brännpunktenParabola 3 a) Punctul A are coordonatele − ,0 2 3 şi , 2 3 2 = p ecua Ńia parabolei este y2 =6x b) A (0,0), ecua Ńia directoarei x =0 şi ecua Ńia parabolei este পিকিউ যদি প্যারাবোলার কেন্দ্রবিন্দু হয়`y=x^(2)2x3`যেমন যে`P=(2,3
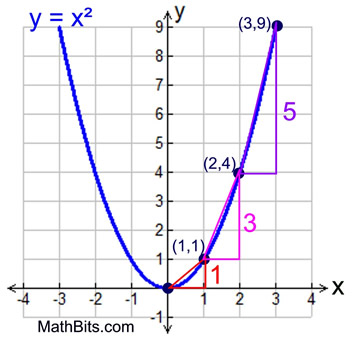



Quadratic Function Rate Of Change Mathbitsnotebook A1 Ccss Math




Solved 4 For The Parabola Y X 2 3 A Does It H Chegg Com
M= 1/3 (two answers ) y^2=12x ;Y=x^2x3 find the X intercept for The parabola define by this equation This should do import matplotlibpyplot as plt import numpy as np # create 1000 equally spaced points between 10 and 10 x = nplinspace (10, 10, 1000) # calculate the y value for each element of the x vector y = x**2 2*x 2 fig, ax = pltsubplots () axplot (x, y) This is your approach with as few changes as possible to make it work




Answered Parabola Y 4x X At The Point 1 3 Bartleby
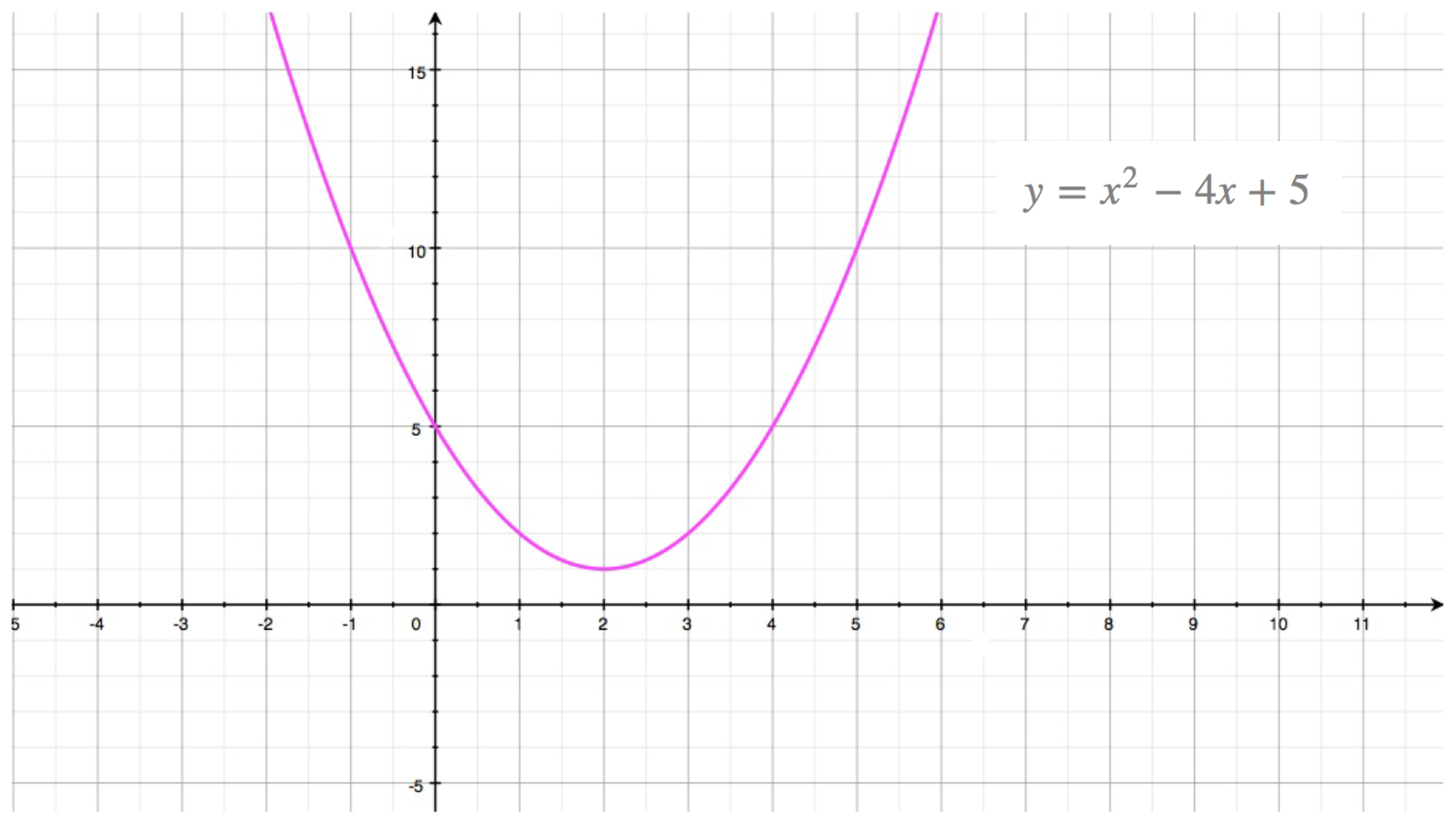



Quadratic Function Parabola
53 Applications of the Parabola A parabola that is rotated around its axis of symmetry to create a three dimensional object is called a paraboloid One of the special properties of a parabola is that any light (or other electromagnetic wave) striking the interior of the parabola the vertex of this parabola is at (2 3) When the y value is 2, the x value is 5 What is the coefficient of the squared term in the parabolas equation Categories English Leave a Reply Cancel reply Your email address will not be published Required fields are marked *Notice, Solving the equation of straight line y=kx1 & equation of the parabola y=x^23 kx1=x^23\iff x^2kx4=0 Now, the line will touch the parabola if both real roots of the above Notice, Solving the equation of straight line y = k x − 1 & equation of the parabola y = x 2 3 k x − 1 = x 2 3 x 2 − k x 4 = 0 Now, the line will touch the parabola if both real roots of the above
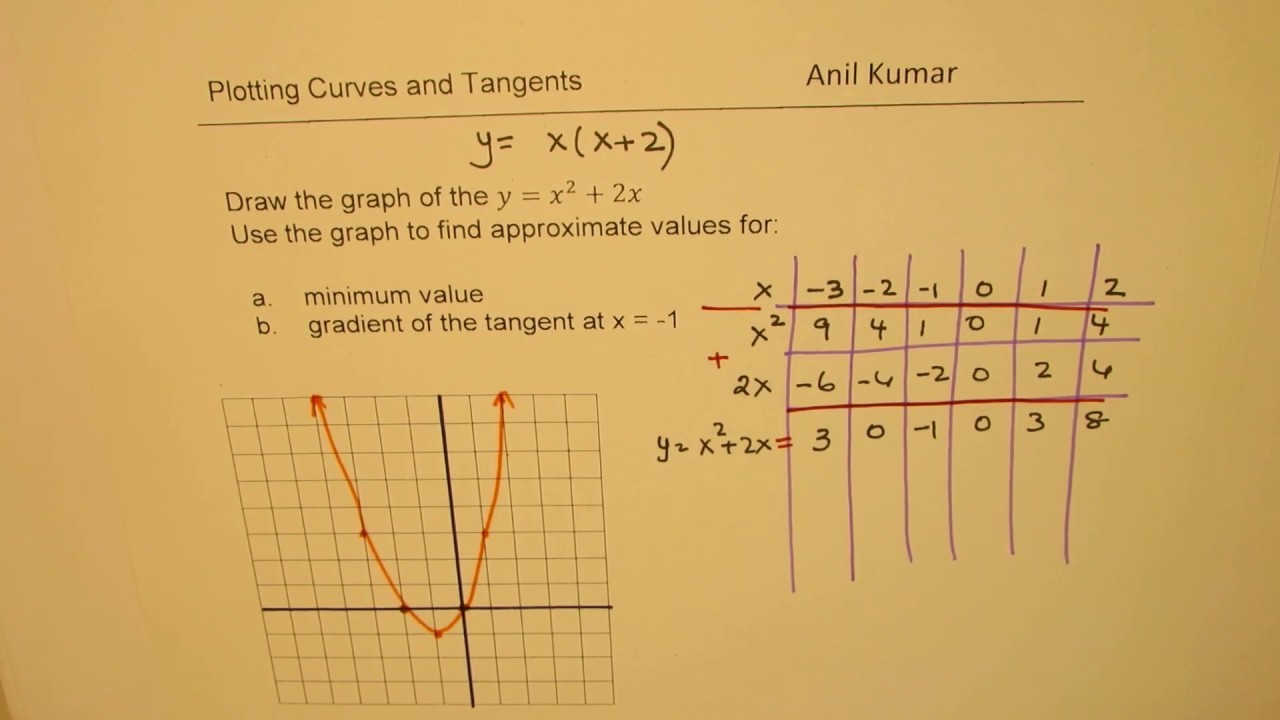



Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube




Please Help The Vertex Form Of The Equation Of A Parabola Is Y X 3 2 36 What Is The Standard Brainly Com
In this section we will be graphing parabolas We introduce the vertex and axis of symmetry for a parabola and give a process for graphing parabolas We also illustrate how to use completing the square to put the parabola into the form f(x)=a(xh)^2kCalculadora gratuita de la directriz de una parábola Calcular la directriz de una parábola dada su ecuación paso por pasoComplete the square for x 2 − 3 x 2 3 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = 0, c = − 3 a = 1, b = 0, c = 3 Consider the vertex form of a parabola a ( x d) 2 e a ( x d) 2 e



Graph Y X 7 X 3 Mathskey Com



Exploration Of Parabolas
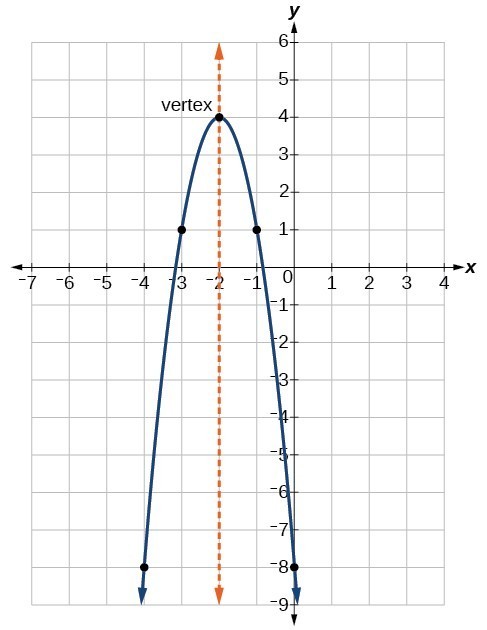
Example 3 Graph y = 2x2 4x 5 Solution Because the leading coefficient 2 is positive, note that the parabola opens upward Here c = 5 and the y intercept is (0, 5) To find the x intercepts, set y = 0 In this case, a = 2, b = 4, and c = 5 Use the discriminantClick here👆to get an answer to your question ️ The equation y^2 3 = 2( 2x y) represents a parabola with vertex at In y = x^2 we're done, that is the y value In y = (x2)^2, after we square, we are done, that is the y value In y = (x2)^2 3, after we square, we still need to subtract 3 from the number, that moves us down 3 The vertex of y=x^2 is the point (0,0) The
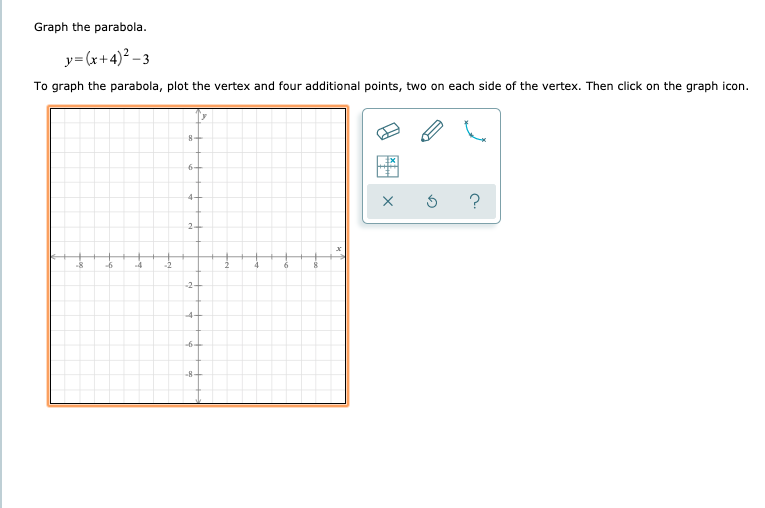



Graph The Parabola Y X 4 2 3 To Graph The Chegg Com



Quadratics Graphing Parabolas Sparknotes
Find the area in the first quadrant bounded by the parabola y^2 = 4x, x = 1, and x = 3 Problem Answer The area in the first quadrant bounded by the parabola and lines is 5595 sq units Solution Latest Problem Solving in Integral Calculus divfeedburnerFeedBlock ul li {background #E2F0FD;I have an equation right here it's a second degree equation it's a quadratic and I know it's graph is going to be a parabola this was a review that means it looks something like this or it looks something like that because the coefficient on the x squared term here is positive and it's going to be an upwardopening parabola and I am curious about the vertex of this parabola and if I haveThe children are transformations of the parent Some functions will shift upward or downward, open wider or more narrow, boldly rotate 180 degrees, or a combination of the above Learn why a parabola opens wider, opens more narrow, or




The Graph Of The Parabola Y 2 X 3 2 4 Has A Vertex Of 3 4 If This Parabola Is Shifted 5units To Brainly Com




Quadratic Function
Graph each parabola y=x^{2}3 Join our free STEM summer bootcamps taught by experts Space is limitedHow do i graph the parabola y=2x^25x3 The area inside the parabola 5x^2y=0 but outside the parabola 2x^2y9=0 is 12sqrt(3)s qdotu n i t If the line y √3x 3 = 0 cuts the parabola y^2 = x 2 at A and B, then PA PB is equal to where, P = (√3, 0)




How Long Does A Firework Ppt Download




Focus Of The Parabola Y 2 2 X 3 Is Youtube
y = x 2, where x ≠ 0 Here are a few quadratic functions y = x 2 5;Examples (y2)=3(x5)^2 foci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=x^{2}2x3Y=3x^2 Calculadora para parábolas Symbolab Calculadora gratuita para parábolas Calcular los focos de una parábola, sus vértices, ejes y su directriz paso por paso This website uses cookies




How To Draw Y 2 X 2
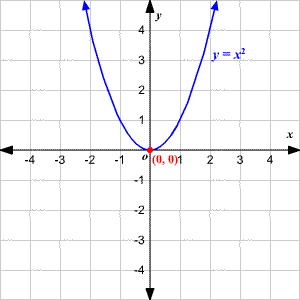



Parabolas
The plot can be obtained by reflecting the function y=x^2/2 about the 45degree line MetaPost, TikZ) use a plot to draw the parabola So they use a lot of segments to approximate it In the spirit of this answer I want to advocate to use a single quadratic (cubic)Free Parabola calculator Calculate parabola foci, vertices, axis and directrix stepbystep This website uses cookies to ensure you get the best experience1= m 1/2 /(1 1/2m) ;
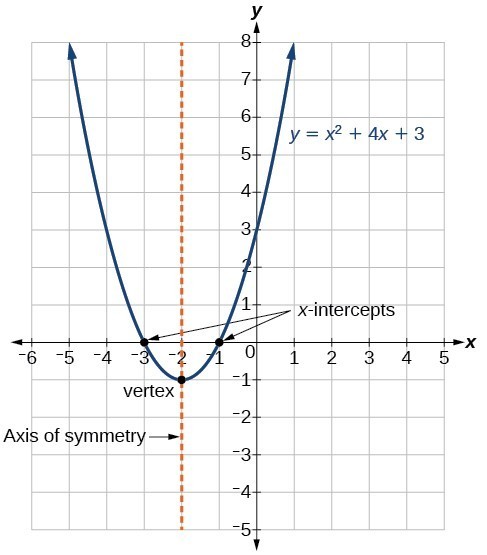



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Geometric Solution Of X X 3 9 36 As The Intersection Of The Download Scientific Diagram
Y = x 2 3x 13; Standard Equation of Parabola The simplest equation of a parabola is y 2 = x when the directrix is parallel to the yaxis In general, if the directrix is parallel to the yaxis in the standard equation of a parabola is given as y2 = 4axSe muestra la ecuacion de una parabola en su forma reducida (y3)^2=12(x1) Se determina vertice, foco y recta directriz de la parabola Se realiza un bocet
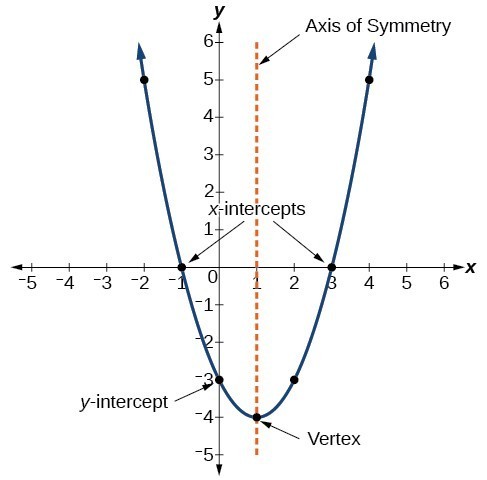



Characteristics Of Parabolas College Algebra



Graphing Quadratic Functions
Answer S = 366 One of the components of a person's success in our time is receiving modern highquality education, mastering the knowledge, skills and abilities necessary We have a formula to find easily the abscissa of a vertex of a parabola Abscissa of vertex of #p(x) = b/(2a)# # # # # # # Let #f(x)=x^23# Then, the vertex of #f(x)# is when #0/2=0# # # And #f(0) = 3# # # # # Therefore the vertex of #f(x)# is #3# when #x=0# Because #a>0# here, the vertex is a minimum graph{x^23 5, 5, 034, 466} 👍 Correct answer to the question Which of the following equations will be the graph of a parabola?




The Tangent To A Parabola Are X Y 0 And X Y 0 If The Focus Of The Parabola Is F 2 3 Then The Youtube
%5E2+3.gif)



Y 3 X 2 Graph Novocom Top



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora
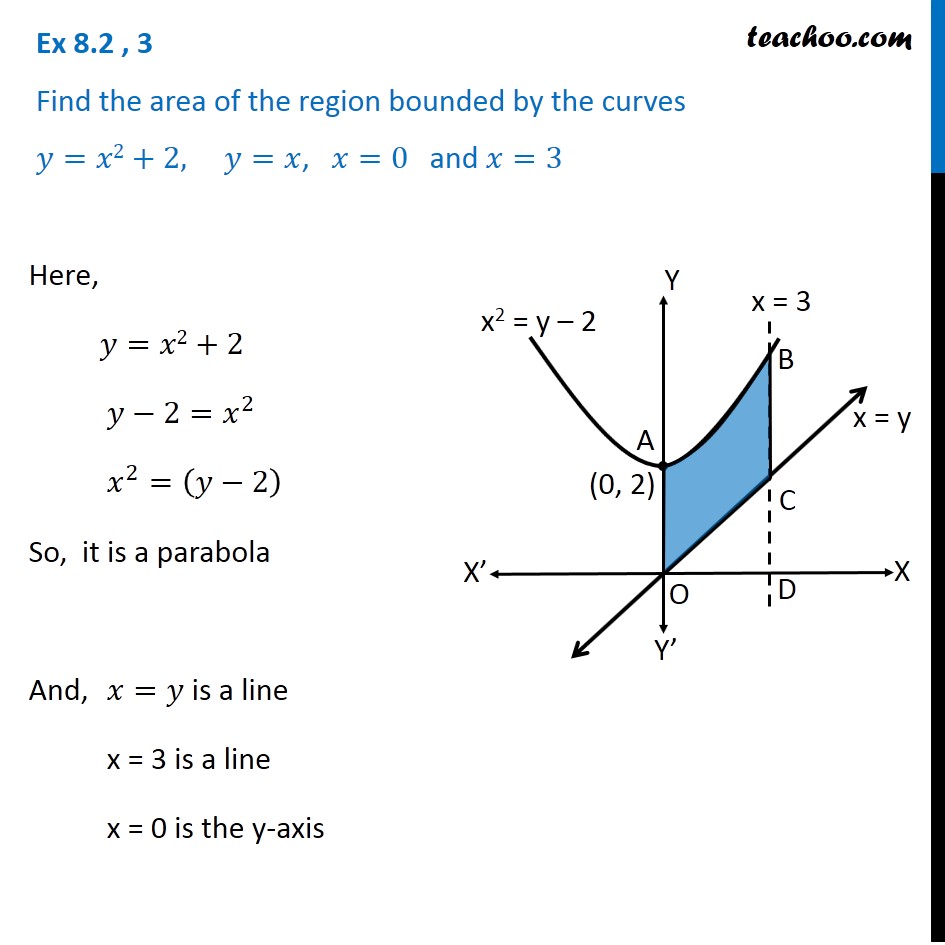



Ex 8 2 3 Find Area Bounded By Y X2 2 Y X X 0 3



1



Graphing Quadratic Functions



Graph The Parabola Y X 2 6x Mathskey Com



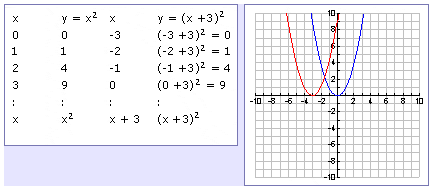
Intro To Quadratic Graphs Key Features Of Parabolas Expii




What Is The Axis Of Symmetry For The Parabola Y Chegg Com



What Is The Equation Of The New Parabola Created By Shifting Y X2 Three Units In The Positive Y Axis Direction Quora



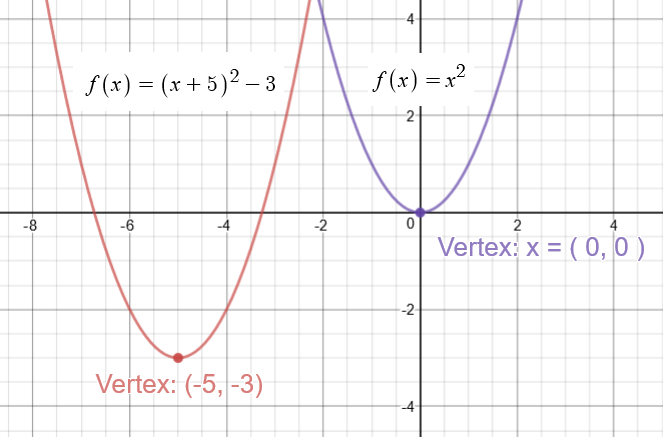
Transformations



How To Graph A Parabola Y X 5 2 3 Socratic



Graphing Quadratic Functions
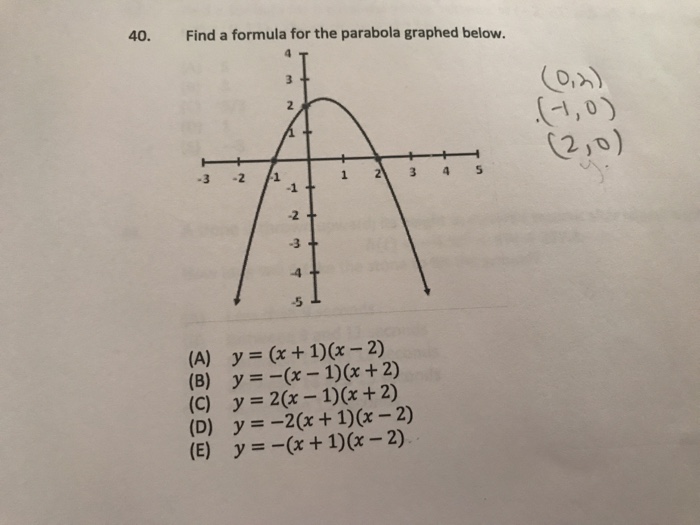



40 Find A Formula For The Parabola Graphed Below Chegg Com




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com



1




Area Between Curves The Parabola Y 3 X 2 And Line Y X 1 Youtube
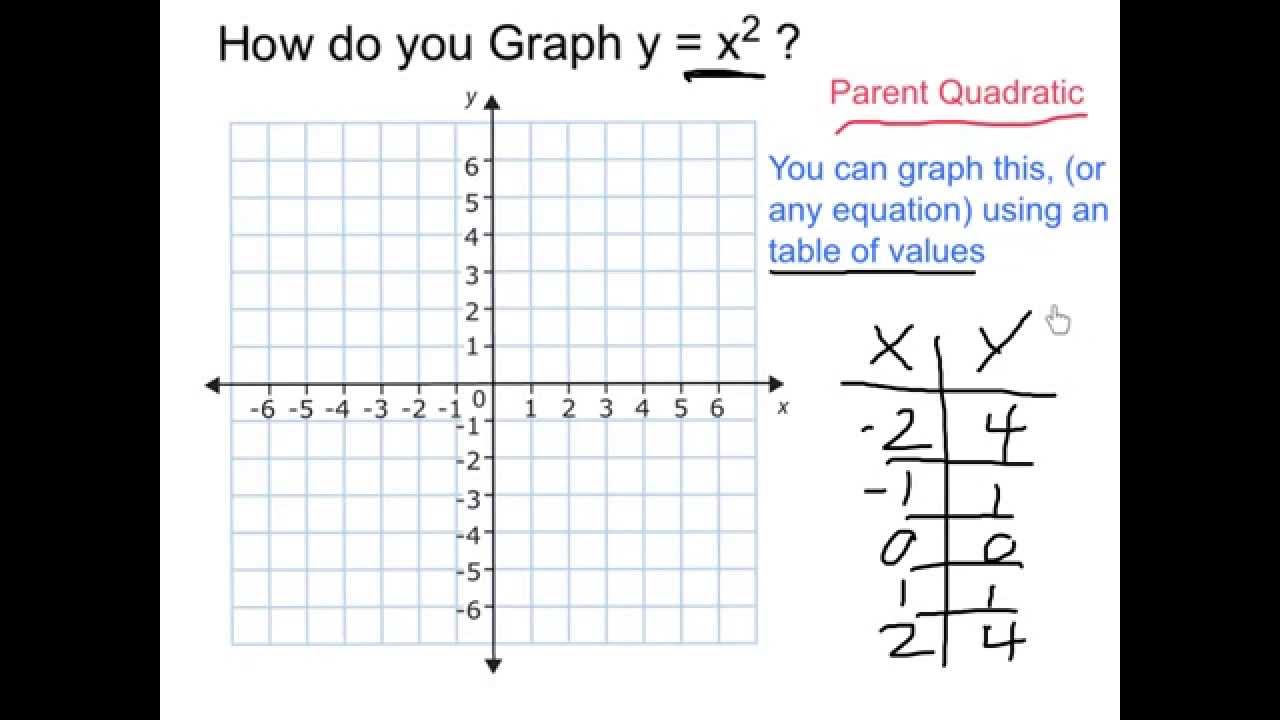



Graph Y X 2 Youtube




X 2 Vs X 3 Graph Novocom Top
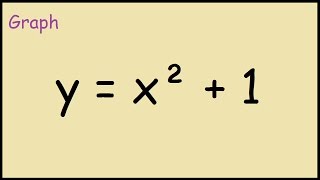



How To Graph Y X 2 1 Youtube



Parabolas




Draw The Graphs Of Following Quadratic Functions I Y X 2
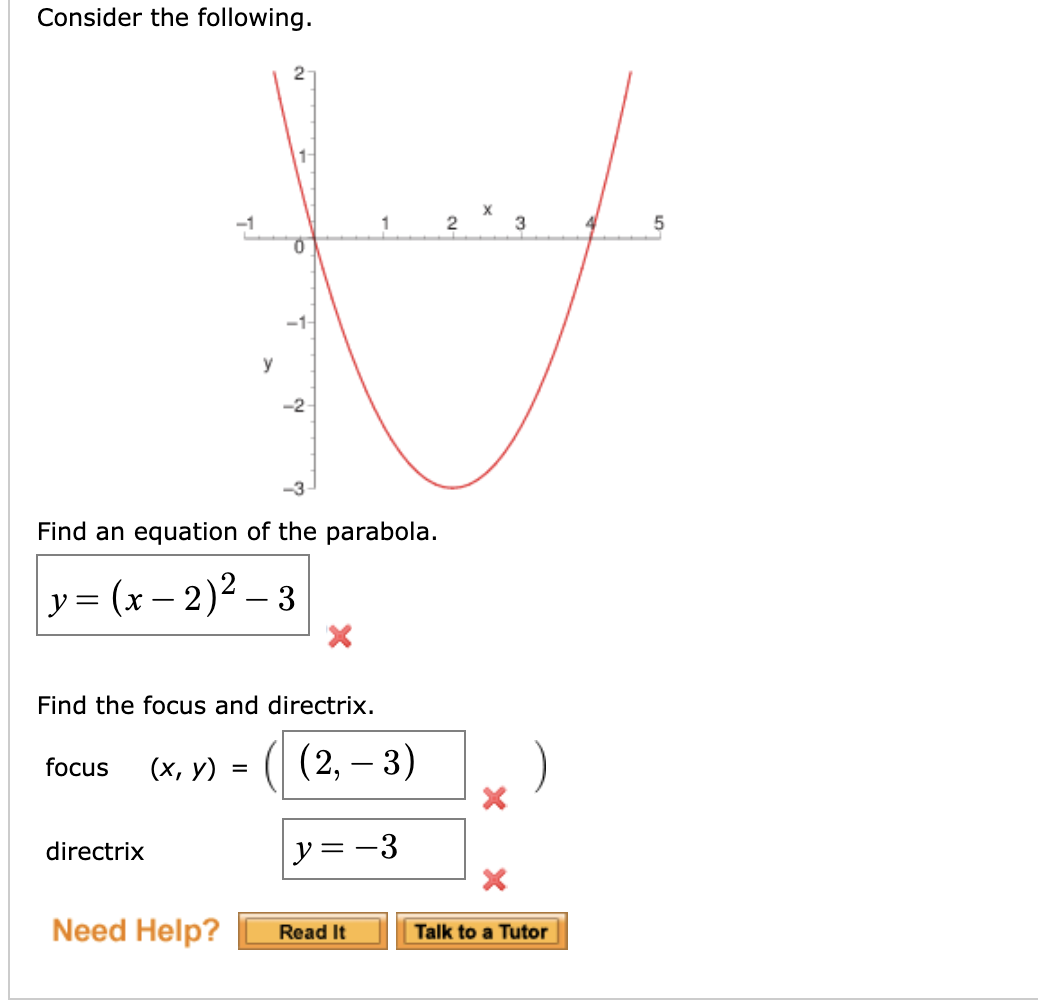



Consider The Following 3 5 1 Y 2 3 Find An Chegg Com
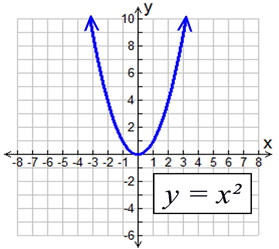



Parabola Parent Function Mathbitsnotebook A1 Ccss Math



Quadratic Functions




The Distance Between The Vertex Of The Parabola Y X 2 4x 3 And The Centre Of The Circle X 2 9 Y 3 2 Is



How To Graph A Parabola Of Y X 1 X 5 Mathskey Com




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic




5 3 The Graphs Of Quadratic Equations X



With Math Ax 2 Bx C Math Why Is The Math X Math Value Of The Vertex Of This Parabola Equal To Math B 2a Math Quora



Square And Cube Function Families Read Algebra Ck 12 Foundation
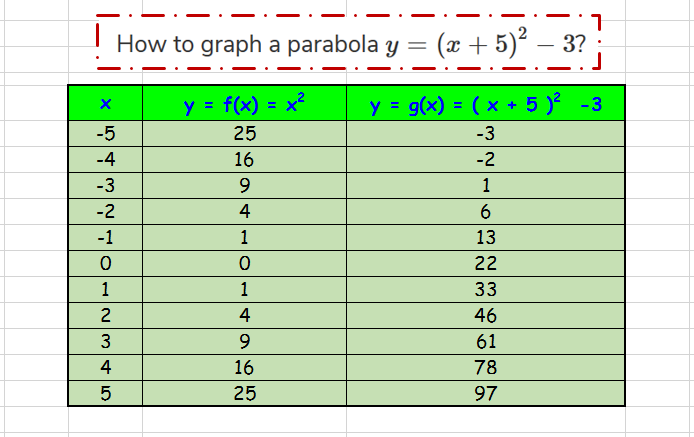



How To Graph A Parabola Y X 5 2 3 Socratic




Quadratic Systems A Line And A Parabola Video Khan Academy




Graphing Parabolas



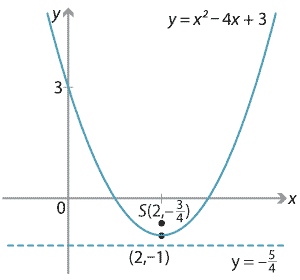
Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Graph Y X 2 Study Com



Graphing Quadratic Functions



Math Spoken Here Classes Quadratic Equations 3




5 2 Properties Of Parabolas Ppt Video Online Download



Content Focus Directrix Definition Of The Parabola



Content Transformations Of The Parabola
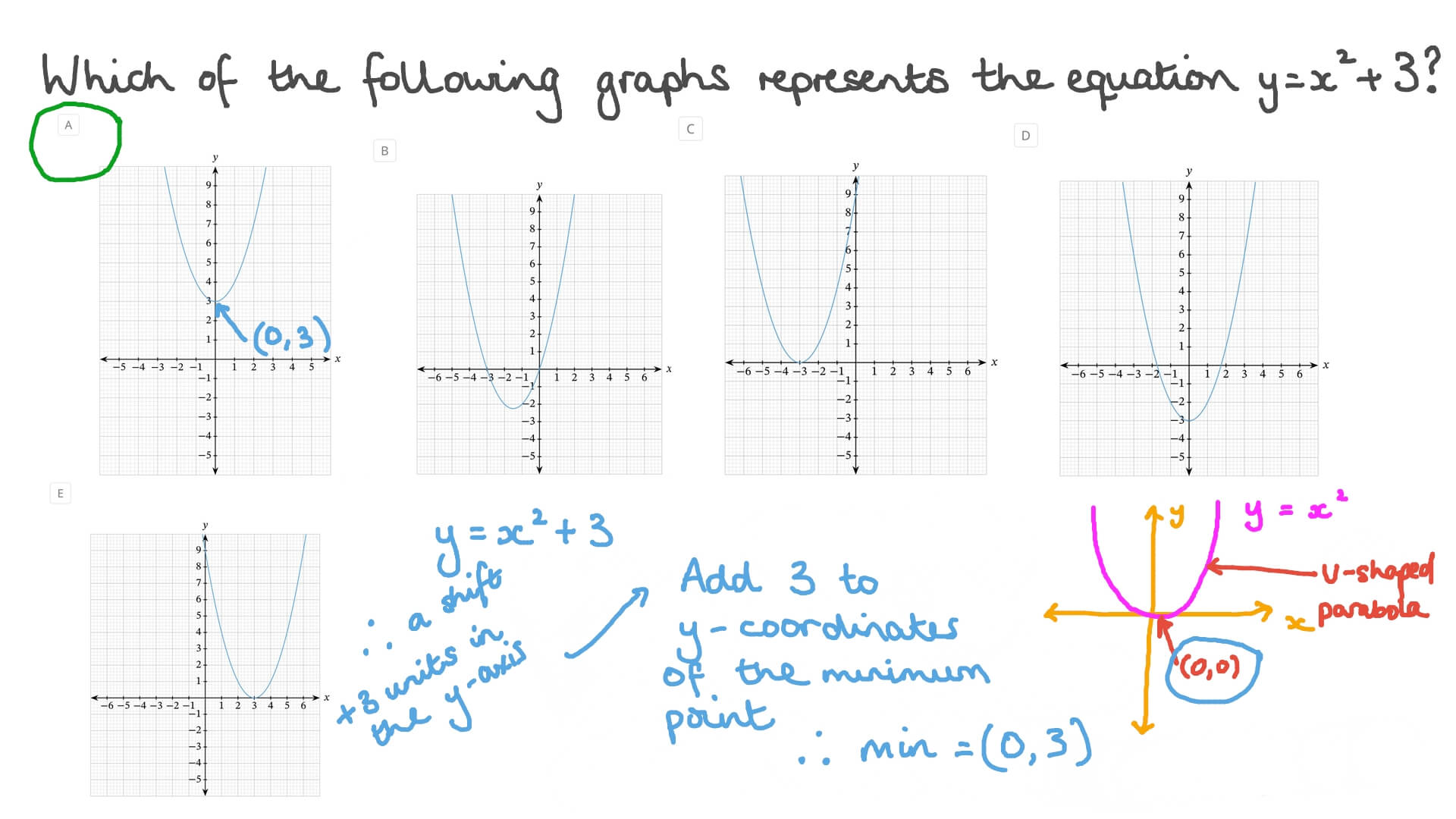



Question Video Identifying Graphs Of Quadratic Equations In Vertex Form Nagwa



Quadratics Graphing Parabolas Sparknotes



Math Spoken Here Classes Quadratic Equations 3




Graphing Parabolas
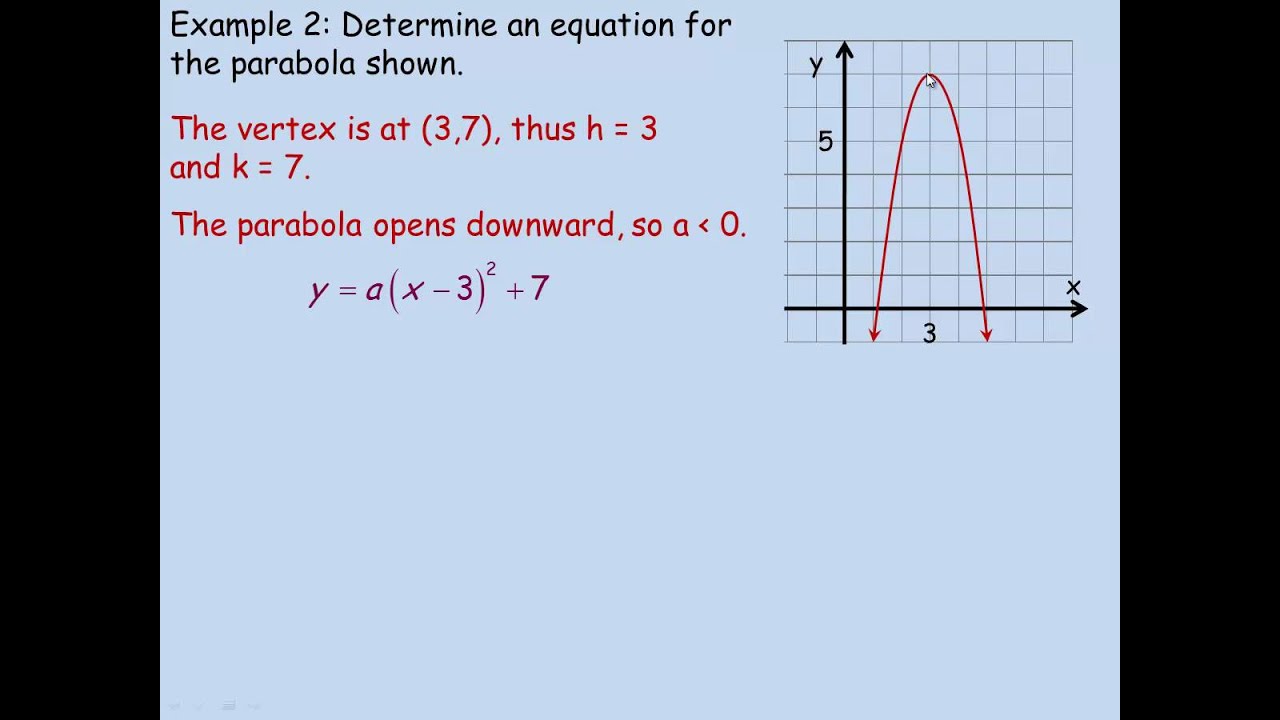



Graphing Y A X H K Youtube
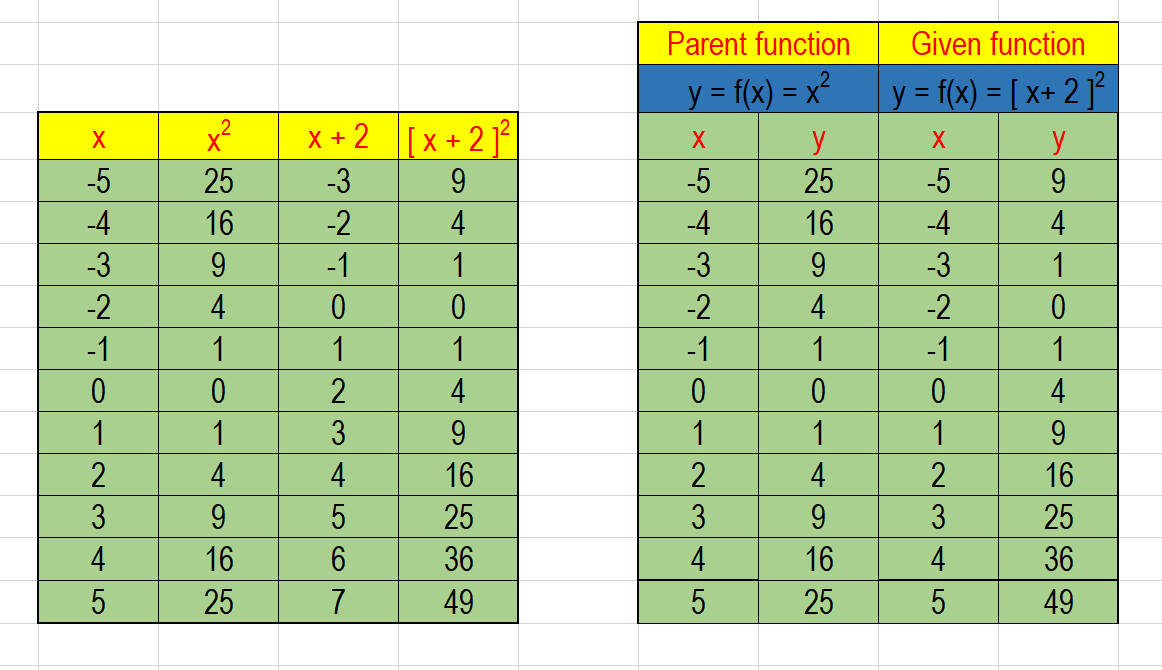



How Do You Sketch The Graph Of Y X 2 2 And Describe The Transformation Socratic
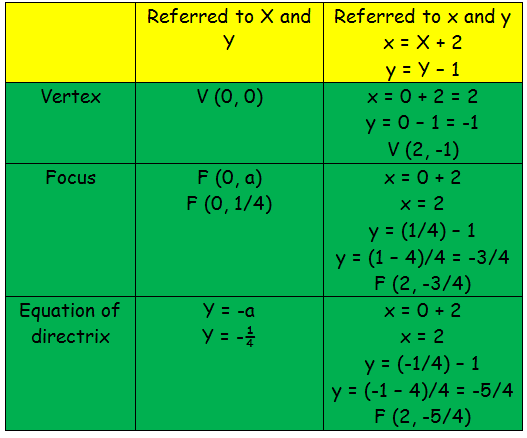



How To Find Focus Directrix And Vertex Of Parabola



Solution The Parabola Y X 2 3 Intersects The X Axis At Two Points P And Q What Is The Distance From P To Q



Where Do Y X 2 4x 1 And Y 3 X Intersect Mathskey Com



Quadratics Graphing Parabolas Sparknotes




The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Which Point Will Satisfy The Brainly Com
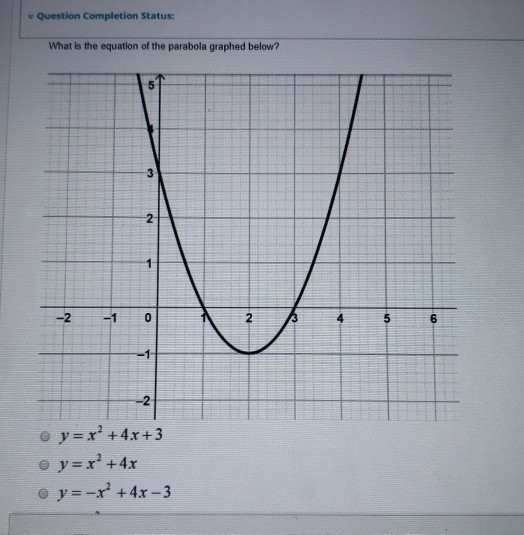



Question Completion Status What Is The Equation Of Chegg Com




Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube



Content Transformations Of The Parabola



Math Spoken Here Classes Quadratic Equations 3




Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Quadratic Function
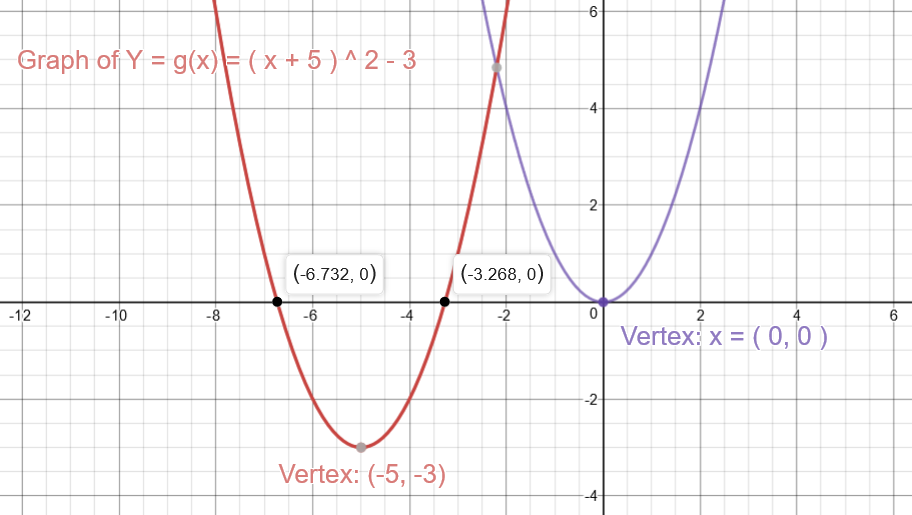



How To Graph A Parabola Y X 5 2 3 Socratic
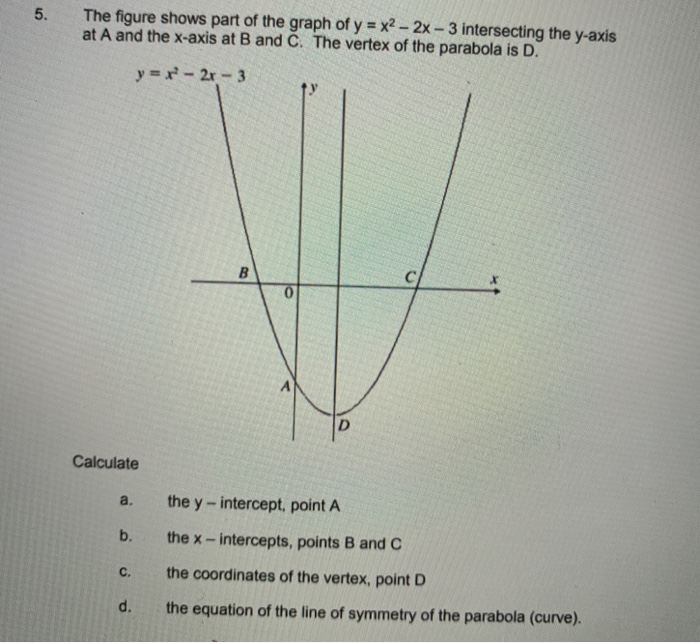



5 The Figure Shows Part Of The Graph Of Y X2 2x Chegg Com




Find The Axis Of Symmetry 1 And The Vertex 2 Of A Parabola Ppt Download



1
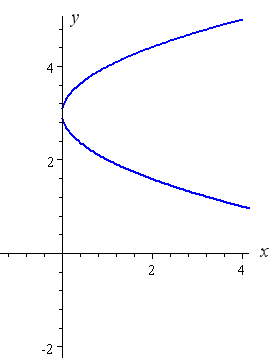



How To Draw Y 2 X 2



The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com
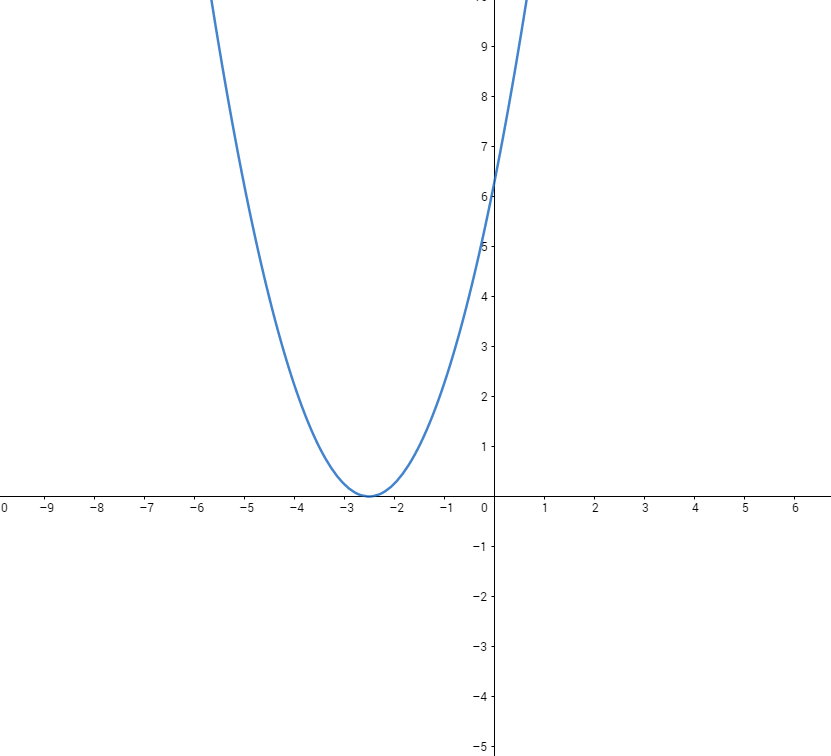



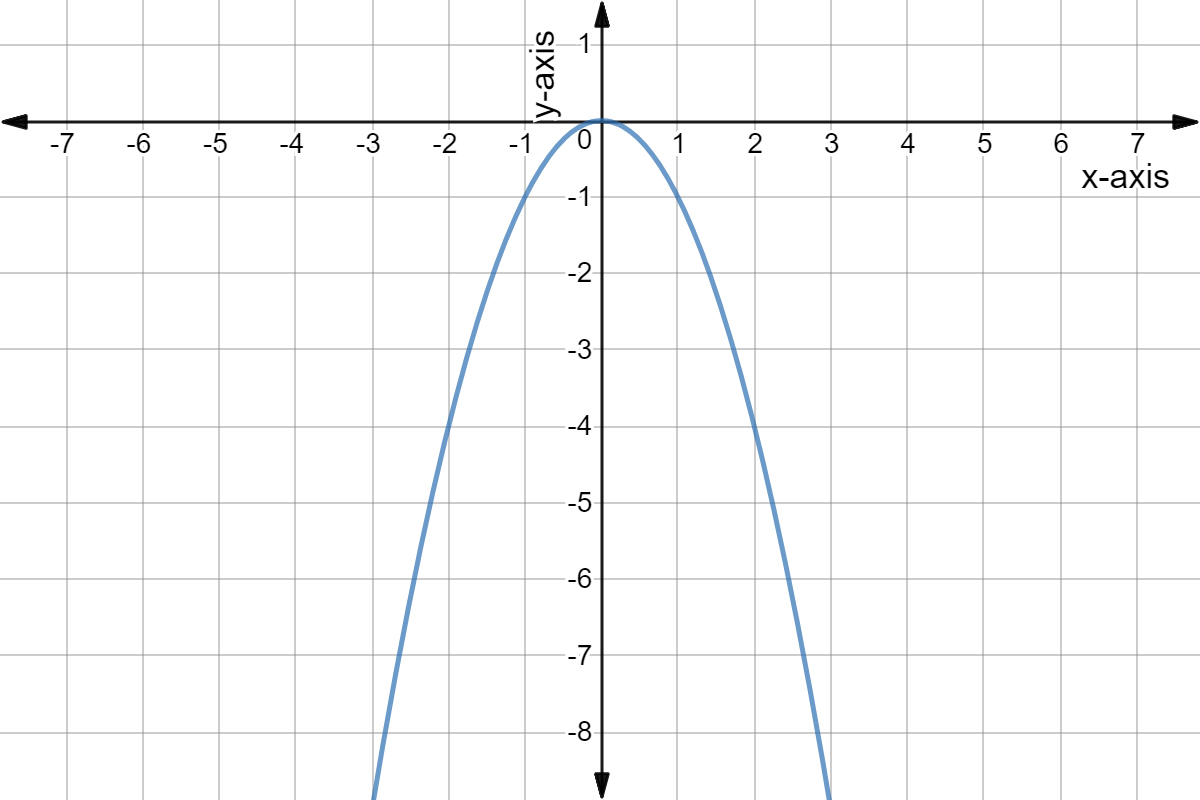
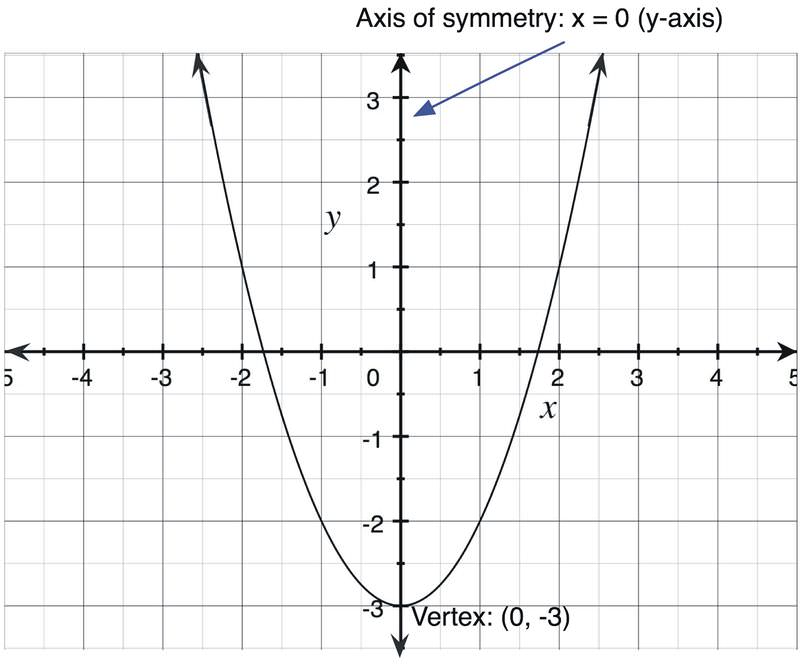
How Do You Graph Y X 2 5x 3 Socratic




How To Graph A Parabola 13 Steps With Pictures Wikihow



Vertex And Intercepts




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation
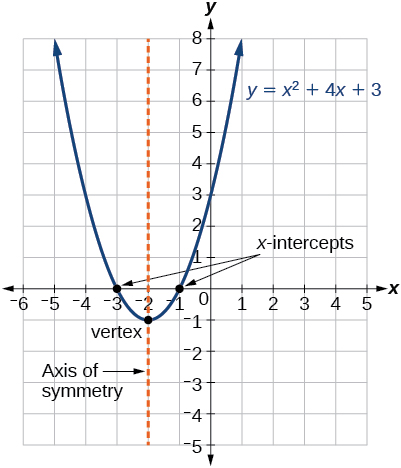



5 1 Quadratic Functions Mathematics Libretexts



Solution Given The Equation Y X 2 7 Calculate The Corresponding Y Coordinates For X 3 1 0 1 3 Please Show All Of Your Work Plot Those Points And Graph The Equation




Quadratic Function




Name Algebra 2 Exam Review Part 2 December 15 All Correct



Y X 2 Graph
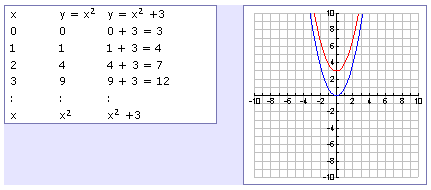



Transformations



Solution How Do You Graph Y X 3 2 2




Shifting Parabolas Video Khan Academy
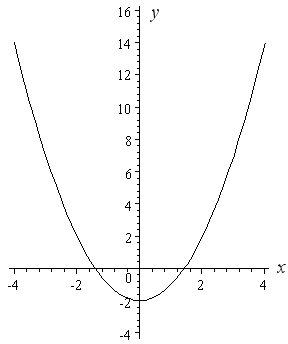



How To Draw Y 2 X 2




Graph Y X 2 3 Youtube



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2




Vertex Axis Of Symmetry Of A Parabola Video Khan Academy
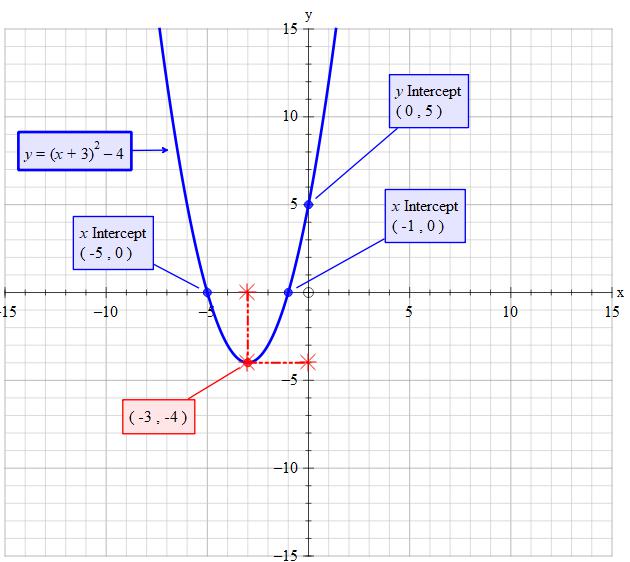



How Do You Find The Vertex And Intercepts For Y X 3 2 4 Socratic



Quadratics Graphing Parabolas Sparknotes



0 件のコメント:
コメントを投稿